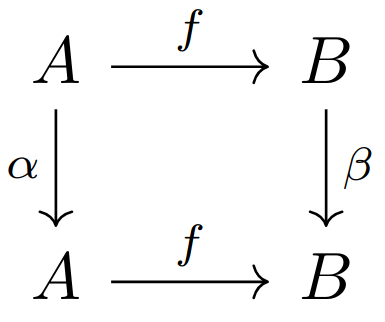参考文献
Conceptual mathematics: a first introduction to categories
第二版序
自从 60 多年前首次引入范畴概念以来,范畴概念已越来越多地应用于数学的各个分支,尤其是在研究不同分支之间的关系时。范畴思想最初产生于对几何与代数之间关系的研究;这些思想的基本简洁性很快使其得到了更广泛的应用。
范畴概念潜藏在初等数学中;明确它们有助于我们走出初等代数进入更高级的数学科学。在本书第一版问世之前,对范畴的简洁描述不得不经由研究生水平的课本才能得到,因为那些例子涉及到模(module)和拓扑空间(topological space)等主题。
我们解决这一难题的办法是从基础出发,发展有向图(directed)和离散动力系统(discrete dynamical system)的概念,只要感兴趣,这些重要的数学结构即便是高中生都可以理解。随着本书的深入,这些结构之间的关系体现了范畴的基本思想。更值得一提的是,即使是图和离散动力系统中的部分细节特征,也被其他连续性更强的范畴——例如其映射由偏微分方程(partial differential equation)描述的范畴所享有。
第一版的许多读者都表示希望能更详细地说明初等范畴质料与更高级应用之间的联系。第二版通过提供两篇新文章和四个附录满足了这一要求。一篇新文章介绍了连通部分的概念,这是在初级图论和高级拓扑学中研究的质的飞跃的基础;这一概念的引入迫使人们认识到函子的作用。附录使用文中的例子来勾画邻接函数在指导数学构造中的作用。尽管这些精炼的附录不能替代对高级课题的更详细研究,但它们将使学生在掌握了课文所学知识的基础上,以更深的理解来进行这类研究。
全书的组织
读者需要注意的是,本书有两种截然不同的“章节”(chapter):
篇章(Article)是本书的骨架;它们大致相当于我们第一次教授课程时给学生的书面材料。
讲解(Session)反映了非正式的课堂讨论,提供了额外的例子和练习。学生如果在文章中的某些练习中遇到困难,往往可以在随后的讲解中解决。我们试图在讲解中保留第一堂课的气氛(甚至学生的名字)。经验丰富的读者只需阅读文章就能获得概览,但会错过许多有启发性的例子和观点。
第一讲是介绍性的。例外的是,第十讲旨在让读者了解更复杂的应用,掌握它对于本书的其余部分并不重要。
每篇文章将在下表所示的后续讲解中作进一步讨论和阐述:
| 篇(article) | 讲(session) |
|---|---|
| 1 | 2-3 |
| 2 | 4-9 |
| 3 | 11-17 |
| 4 | 19-29 |
| 5 | 30-31 |
| 6 | 32-33 |
| 7 | 34-35 |
附录的编写方式较为轻松,旨在快速总结课程基本材料与现代数学各种更先进发展之间可能存在的一些主要联系。
第一讲、伽利略与对象的乘法
1、引入
本书旨在探索一种观察数学本质的新的基础性视角,它能帮助我们更好的理解运用数学概念。尽管这种视角很简单,但却并不为人熟知;你需要付出一些努力来掌握它们,但报偿是丰厚的:它将帮助你洞察任何学科的数学问题。
有一个基本概念深植于其他一切概念,即“范畴”(category),它好比一个“数学宇宙”(mathematical universe)。有各种各样的范畴,每个都适合特定的主题 (subject matter),而且有从一个范畴到另一个范畴的方法。我们将首先非正式地介绍这一概念、举一些例子。我们将看到,对象(object)、映射(map)和映射的复合(composition of maps)都是数学的要素。
虽然数学涉及不同的范畴及其相互关系这一理念(idea)已隐含了几个世纪,但直到 1945 年艾伦伯格和麦克莱恩才在他们的开创性论文《自然等价的一般理论》中给出了这一基本概念的明确定义,综合了数十年来对数学工作及其各部分关系的分析。
2、伽利略与鸟的飞行
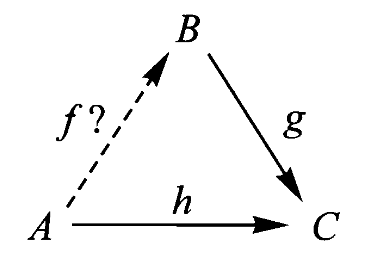
四个世纪以前,伽利略开始思考运动(motion)的问题。他希望理解抛出的石块或喷泉水柱的精确运动。每个人都观察到过那运动遵循的抛物线轨迹,但石头的运动并非仅仅意味着它的轨迹,运动涉及到每个时刻石块的位置。为了记录它,我们需要的是运动图像(motion picture)而非时间曝光(time exposure)。我们说运动是从时间到空间的映射(map)或函数(function)。
这里地图(map)本身就是一种映射,因为它把地理上的真实位置映射到纸面上的位置。
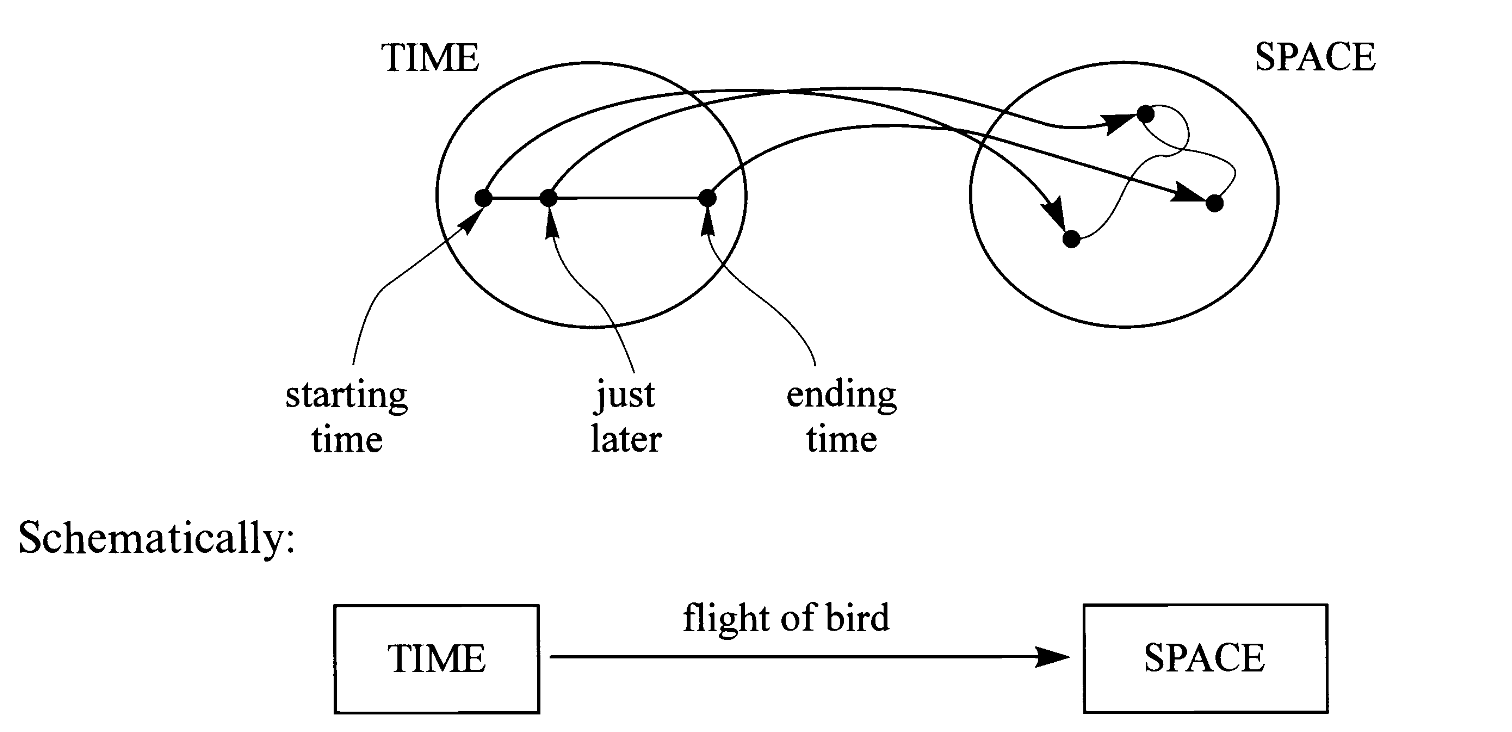
伽利略在比萨斜塔做的自由落体实验,是垂直运动的实验,似乎并不能给一般运动带来多少启发。但为什么伽利略关注这个特殊情形呢?
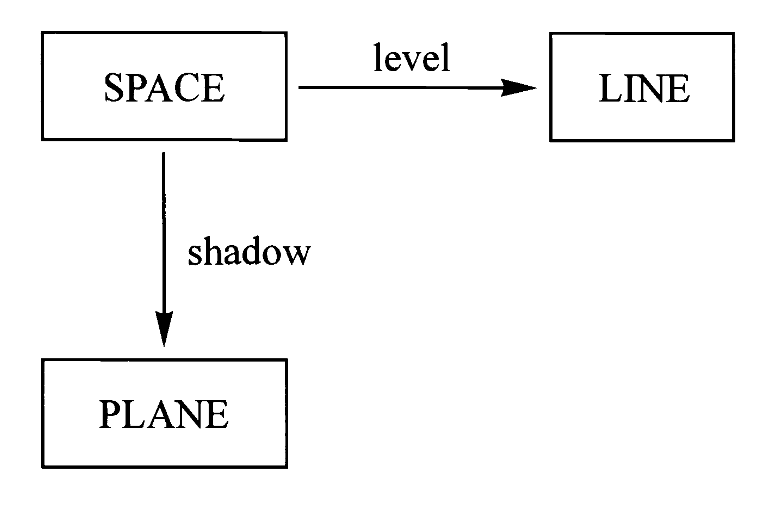
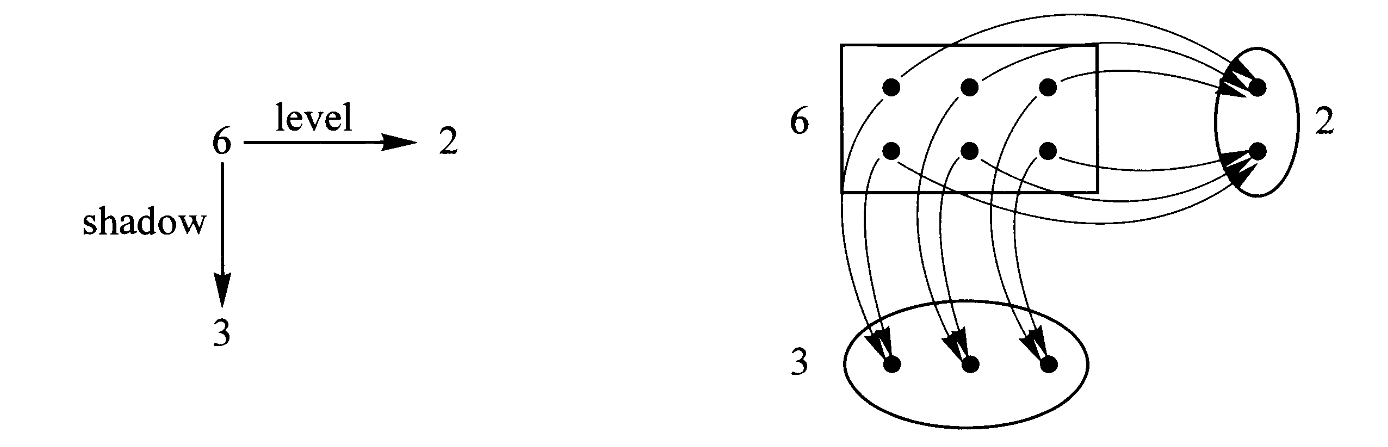
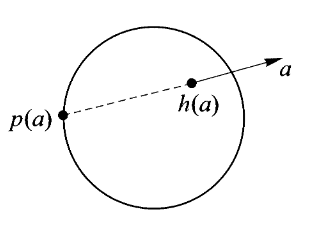
答案是“空间=平面*直线”。但还需要解释,下面是两张图:
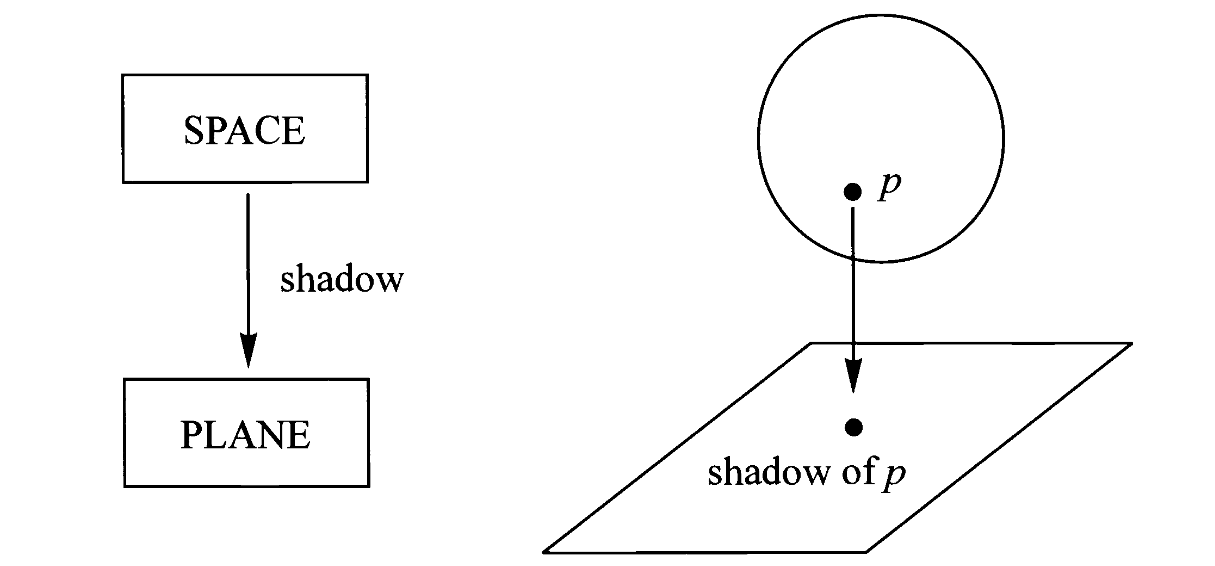
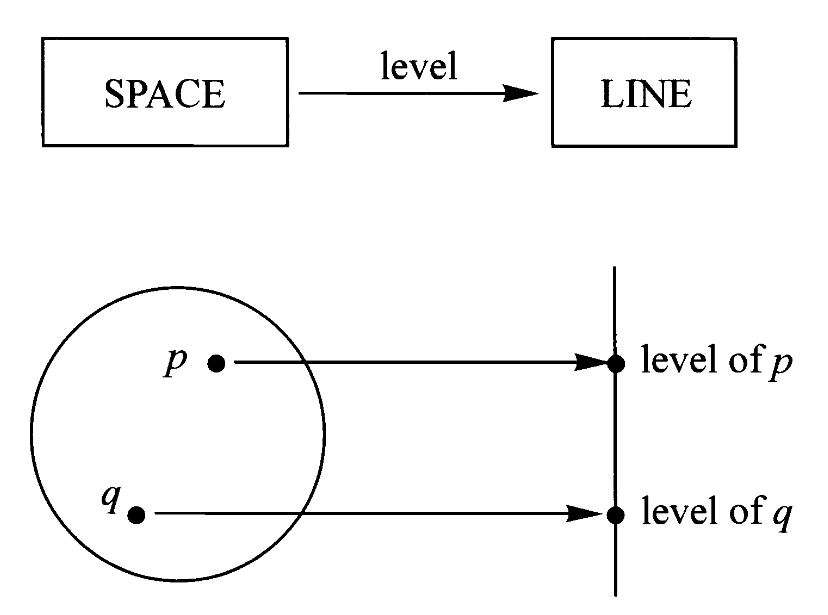
左边我们把空间中的任意一点投影到水平面上的一点,而右边我们把空间中的任意一点映射到直线上的一点。这里我们不妨想象前者是正午太阳直射物体在地面上留下阴影,而后者是在地面上立起竖杆,并标记物体上每一点的水平高度。
由此我们得到了两个映射,分别是“影”(shadow)与“层”(level)。于是我们把每个关于空间的问题变成了两个相对简单的问题,分别关于平面和直线。于是,为了追踪鸟在空间中的飞行,原先我们需要记录时间到空间的映射,现在变成只需要记录时间到平面与时间到直线的两个映射即可。
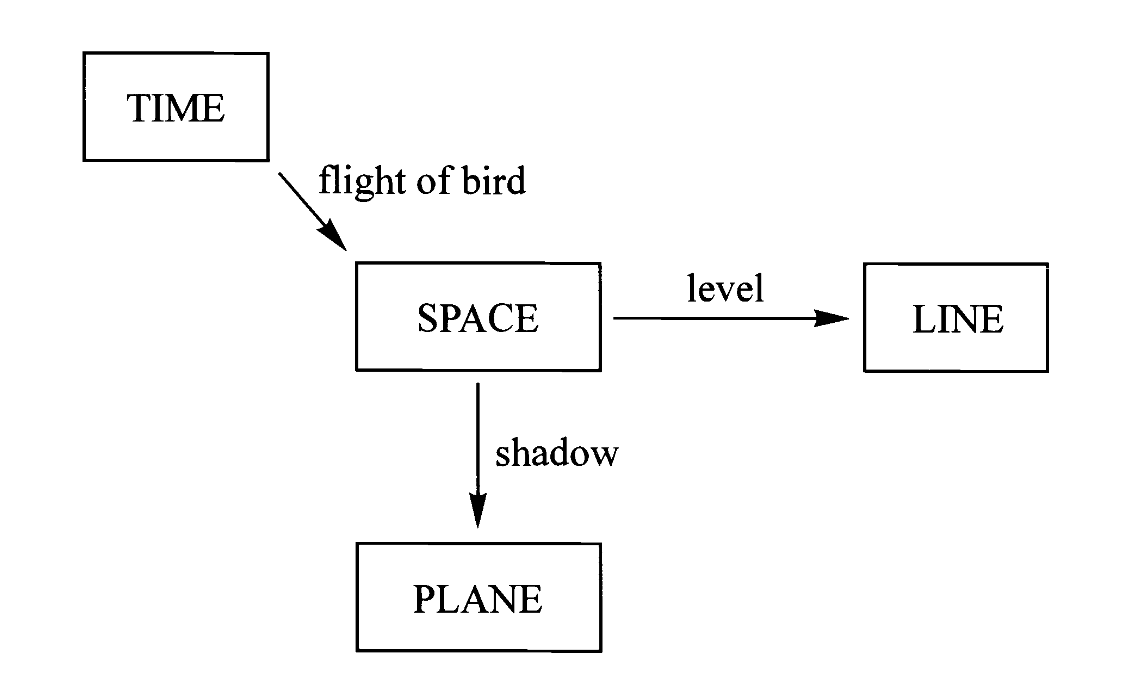
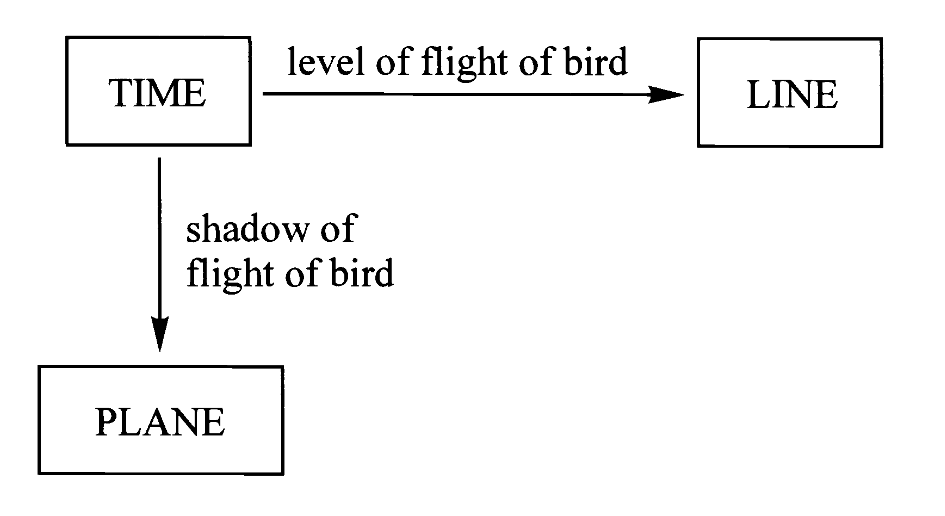
经过这一分解,伽利略发现通过追踪这更简单的两个运动,在空间中的复杂运动可以被彻底重建。因此伽利略得以将一般的运动模式分解为水平运动与垂直运动这两种简单情况。
这一切都归功于把空间通过以上两种映射表示为平面与直线,而这就是我们想说的“空间=平面*直线”。但为什么这两种映射与乘法有关?
对象乘法的其他例子
乘法的身影通常出现在独立选项的背后。譬如餐馆提供两道主食,那么菜单就是两道主食选项的搭配。
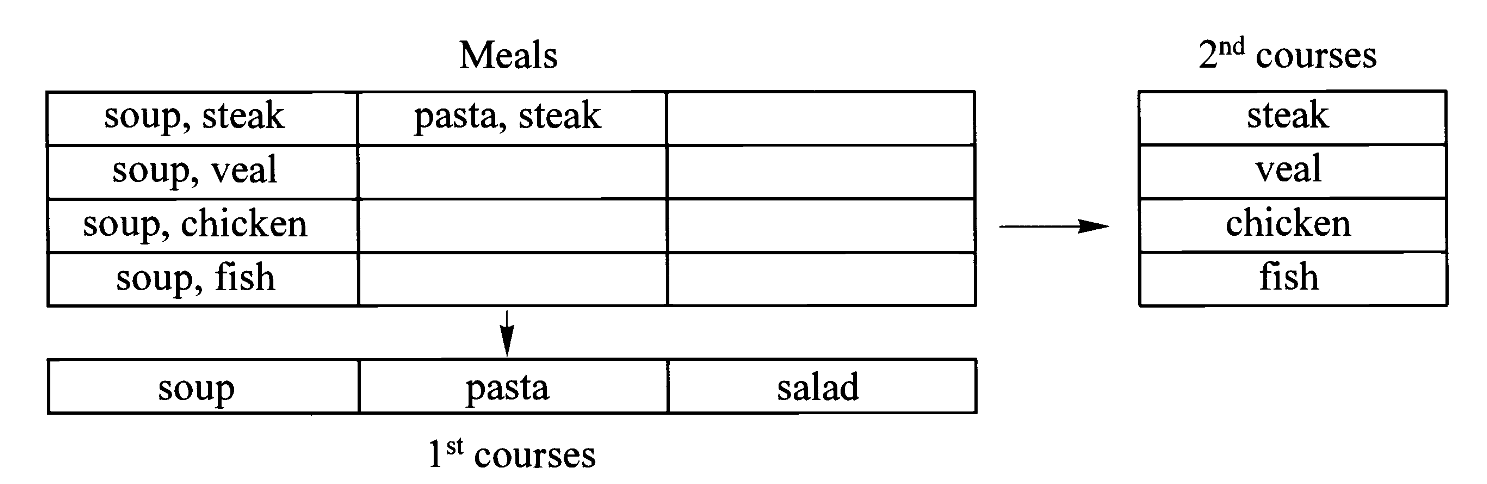
这种关系与伽利略的分解一致。
这种乘积关系还出现在各式各样的情形下,例如几何中线段与圆盘的乘积是圆柱体。我并不是说圆柱的体积等于线段长度乘圆盘面积,而是说圆柱体本身是这个乘积,因为我们可以同样将圆柱体通过两个投影过程将其分解成线段(垂直分量)与圆盘(水平分量)。
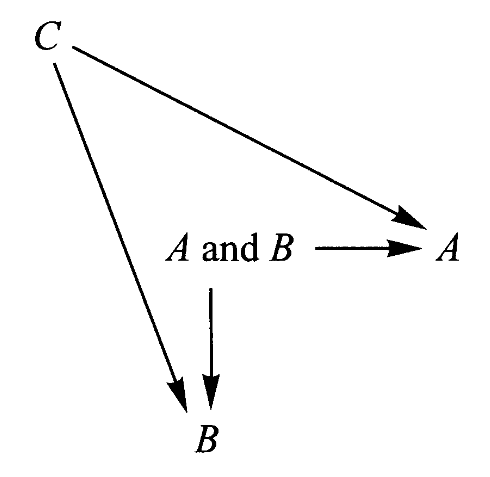
逻辑学中,乘积与并(and)运算联系着。从“A and B”这个语句中,我们能推导出“A”语句与“B”语句。除此以外,从 C 语句推导“A and B”等价于分别从 C 语句推导“A”与“B”两个子句。也即,
最后,乘积与数的乘积的联系。
乘积关系表达的其实是乘子与乘子间的独立性,以及乘子与乘子独立组合得到乘积,即部分如何生成整体的性质。
第一部分、集合范畴
集合的映射是从一个集合到另一个集合的过程。我们研究映射的复合(一个过程接着下一个过程),发现映射复合的运算类似于数的乘法运算,但其解释要丰富得多。
第一篇、集合、映射、复合:范畴的第一个例子
在给出范畴的确切定义前,我们至少需要熟悉一个例子,即有限集合及其映射的范畴。
该范畴中的一个对象 object 是一个有限集合 set 或搜集 collection。例如,在集合范畴中,全班所有学生的集合是一个对象,教室中所有桌子的集合是一个对象,字母表中的 26 个字母的集合是一个对象。
例如一个三元有限集可以表示为
- 确定性:大括号表示将这些元素囊括起来
- 互异性:元素用不同名称指示
- 无序性。
以三个人的集合为例,图示如下
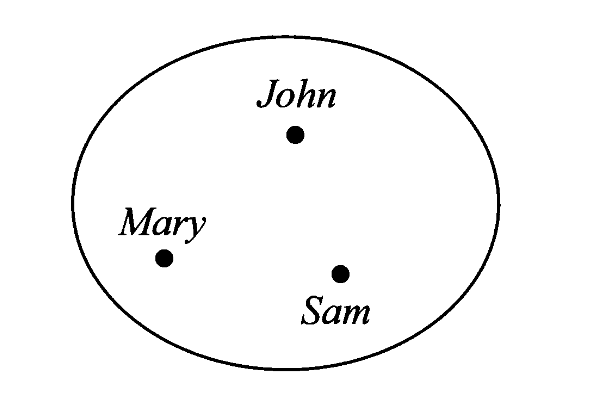
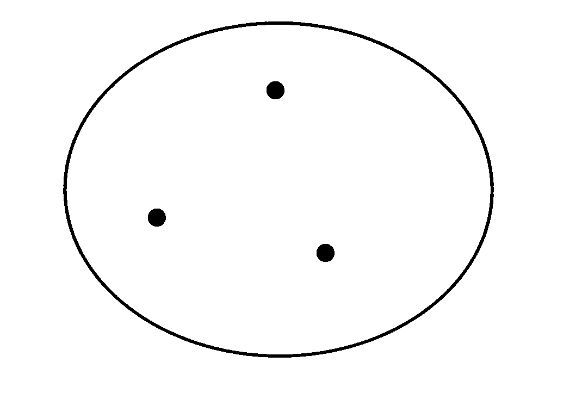
这里确定性由圆圈囊括表示,互异性由空间位置不同的点表示,无序性用非序列化的散点表示。当我们不在乎元素名称时,也可以在图示中略去。这种图示被成为集合的内部图示 internal diagram。
该范畴中的一个映射 map,包含三个东西:
- 集合 A,称为映射的域/定义域 domain。
- 集合 B,称为映射的陪域/值域 codomain。
- 规则,为域中每个元素
分配陪域陪域中的一个元素 ,记为 。
映射的其他名称还有函数 function,变换 transformation,算子 operator,箭头 arrow,态射 morphism。
映射也可以用图示表示,例如上面三人各有最喜爱的早餐:
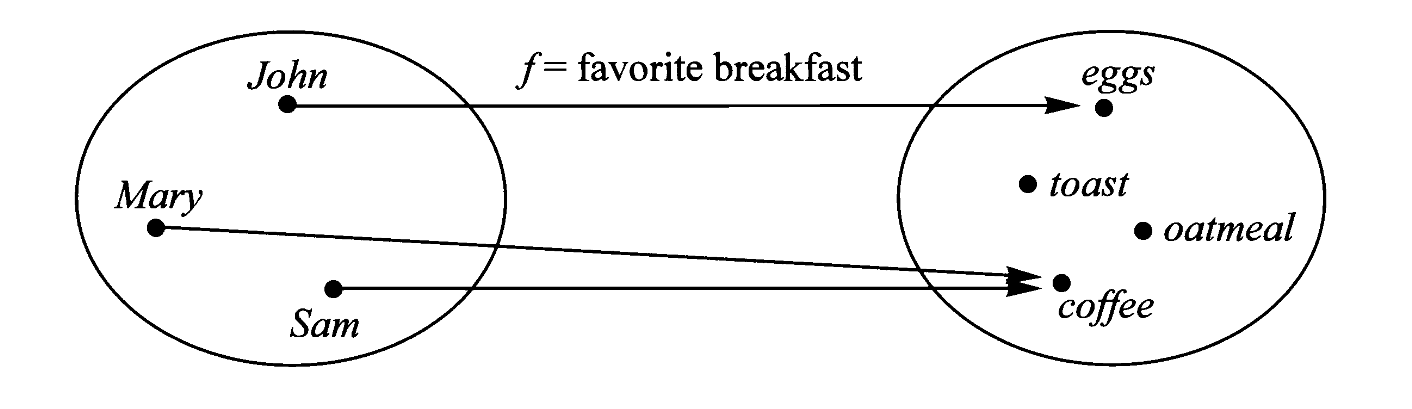
映射表示某人最喜爱的早餐,它将某人映射到它最喜爱的早餐。这被称为映射的内部图示。
注意以上情形的一些特殊之处,它反映了映射的特点:
- 对域中的每个点,都有恰好一个箭头从它出发。
- 对陪域中每个点,可能有任意数目的箭头到达:零,一个或者多个。
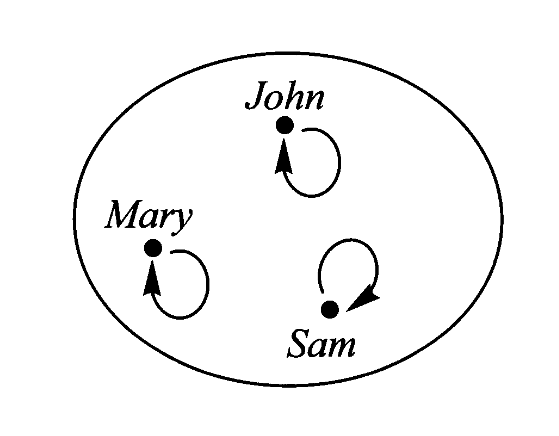
上述讨论并未排除一种特殊情况,即映射的域和陪域可以是同一个集合。例如某人最喜欢的人:
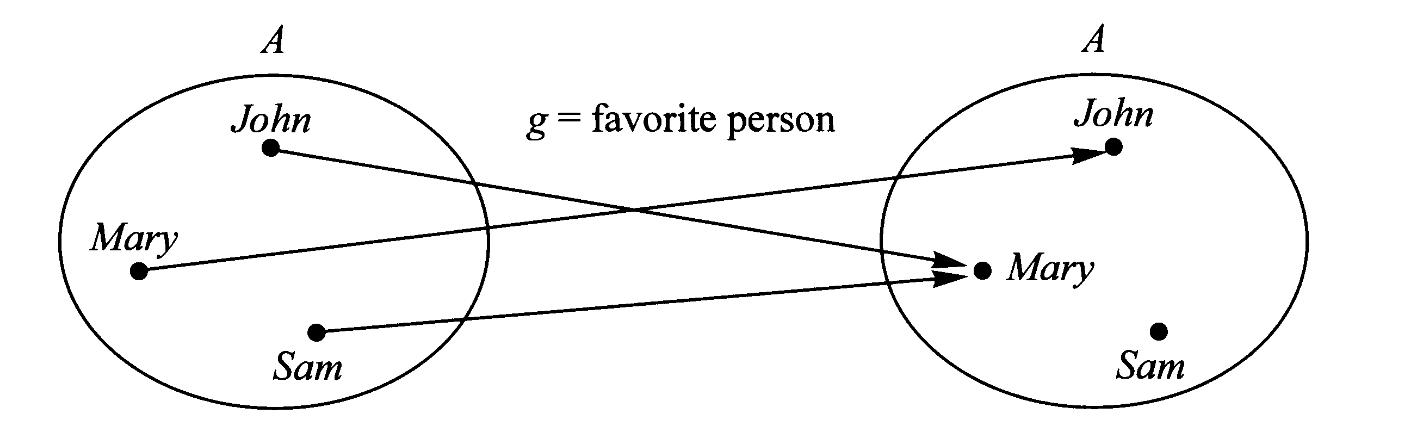
这种映射又被称为*自映射、内映射 endomap。*对自映射而言,其内部图式可以有另一种表示
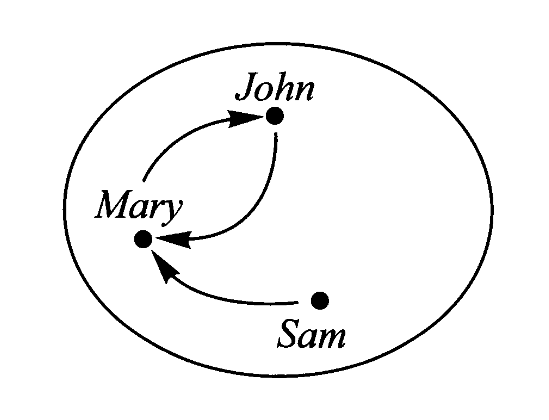
对每个对象 A,存在一个特殊的域与陪域都为 A 的自映射,即恒同映射 Identity map。
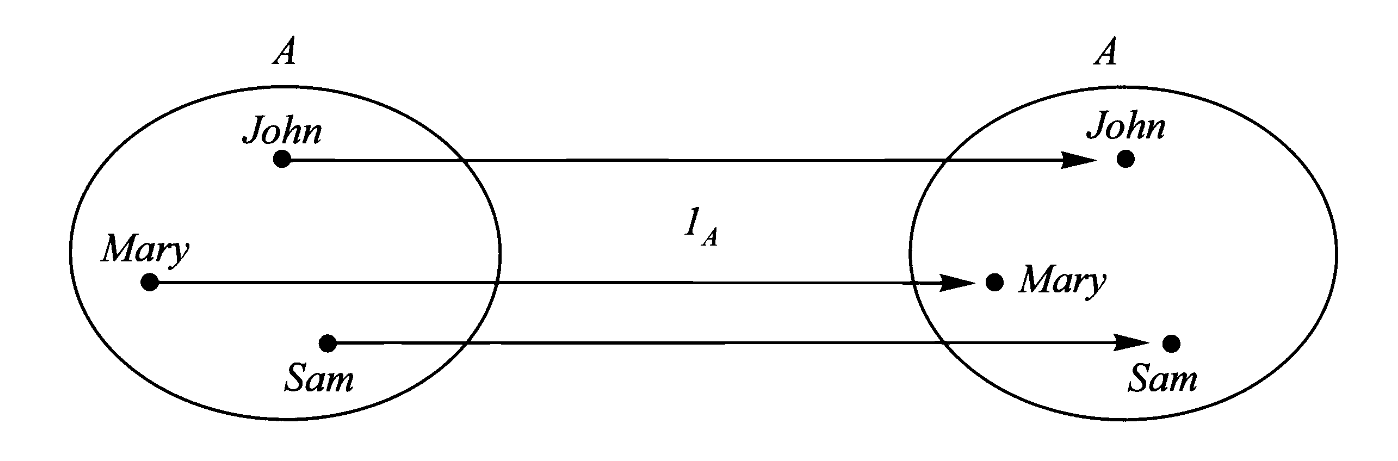
恒同映射
记为
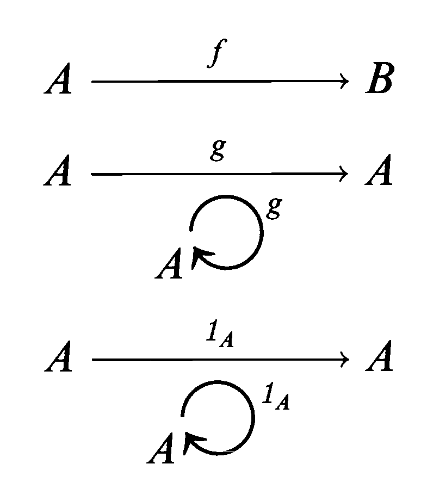
如果我们只需要追踪映射的域和陪域,而暂时忽略图中的其他细节,那么我们就用字母来表示对象,用带符号的箭头来表示映射,这就是外部图式 external diagram。上述五个内部图示所对应的外部图示如下:
映射的复合赋予了范畴概念下的一切动力学(dynamics),通过它两个映射可以结合得到第三个映射。例如把前面每个人喜欢的人与每个人喜欢的早餐复合起来,得到的映射就可以表示每个人为他最喜欢的人应该准备什么早餐?
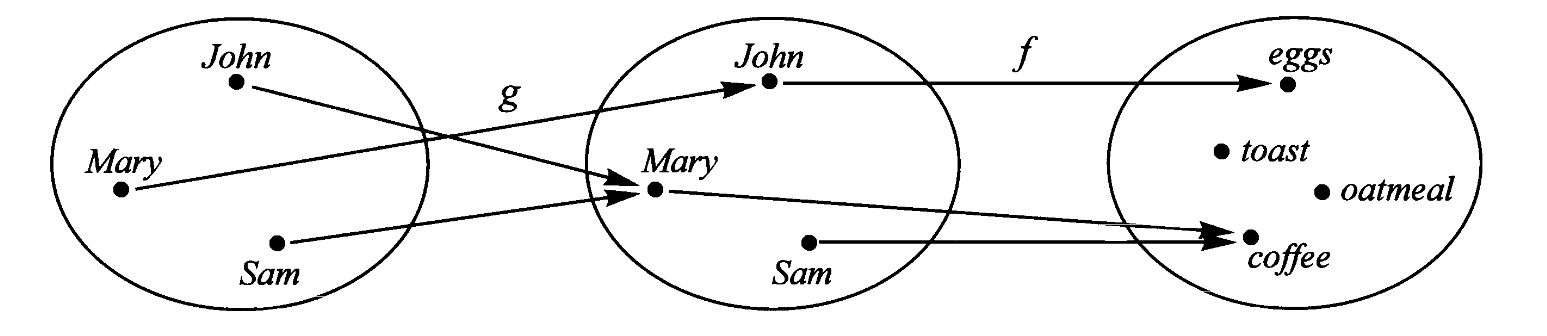
对应的外部图示为
一步到位
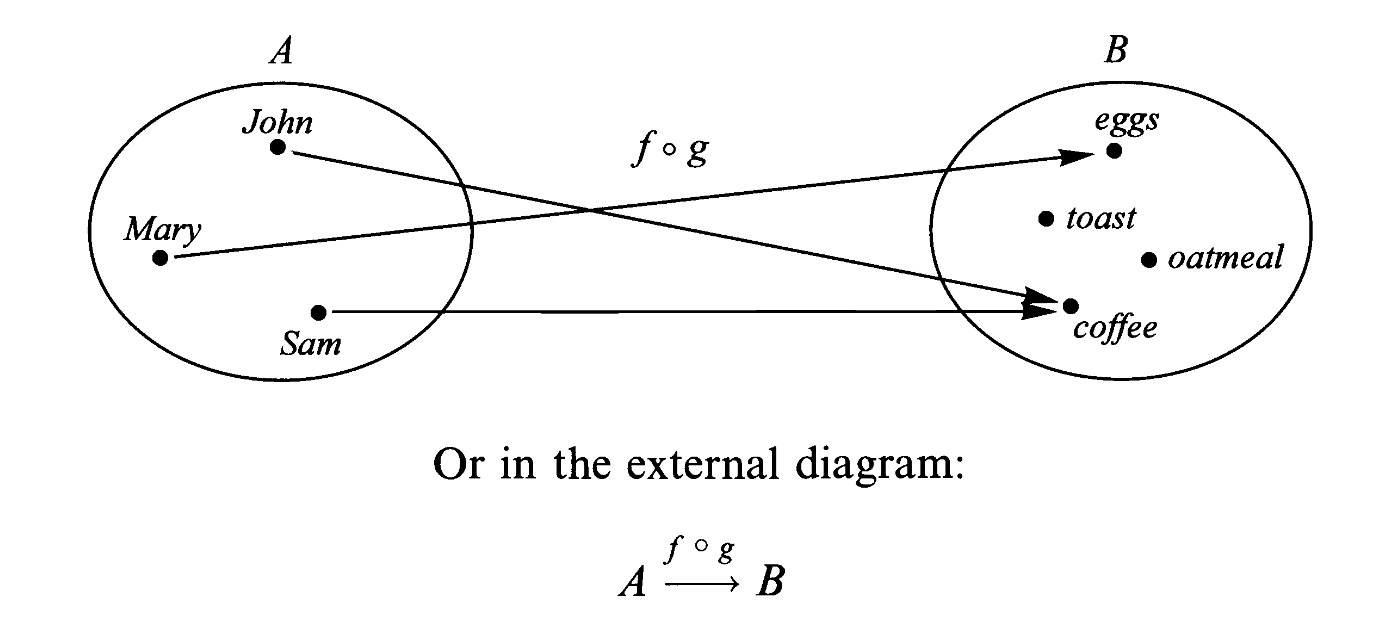
也就是说,如果我们有两个映射,其中一个的陪域恰好是另一个的域,那么我们就可以将其复合得到一个新映射,新映射的域是前者的域,而陪域是后者的陪域。
我们将考察映射的复合与数的乘法的共通之处。注意不要把它与第一讲中与对象的乘积的共通之处混淆起来。
万事俱备了!为了创建一个范畴,我们需要的所有成分都在上面了,总结一下:
范畴中的数据 data
对象:
映射:
恒等映射: (每个对象有一个)
映射的复合:任意两个域与陪域相接的映射
此外这些数据必须服从以下规则,这些规则对应着一致性。
- 恒同律 identity law:
- 若
,则 - 若
,则
- 若
- 结合律 associative law:若
,则
恒同律是恒同映射不会影响对象中元素的恒同性,即使经过“变换”,元素依然是它本身。结合律是映射的结合顺序不影响总体效果,即映射的结合两两之间是独立的,换言之映射只对其域和陪域负责,它并不关心域中的元素经历了怎样的过去,即被怎样的映射或映射复合映射到域中,同时它的影响也止步于陪域,即它不会介入被映入陪域中的元素未来将被如何映射。
也就是说,元素的存在就是其所经历的一切映射历史的凝缩。我们可以说,存在切割了时间,它将错综复杂的历史拓扑切割为序列化的物质,据此我们得以观察到时间(映射逐个作用于对象),物质的存在本身屏蔽了其过往历史,斩断了过去与未来的链接。这与 Markov 链的特点非常相似。
书中给出了这些规则成立的图示,但图示仅仅能够表示特例。其实这些规则是可以证明的。
试举结合律为例,为了证明两个映射相等,根据映射的定义,需要证明其
- 定义域相等:
- 值域相等:
- 规则相等:即任意
, 即可。 我们将映射链分为三份:
根据映射的复合,
(1+2) (2+3) (3+4) (1+5) 于是由 6,7 知 a,b 成立。
记
。由映射的性质 3 和映射的复合定义可知,
单元集(singleton)是含且仅含一个元素的集合。固定一个单元集,称其为

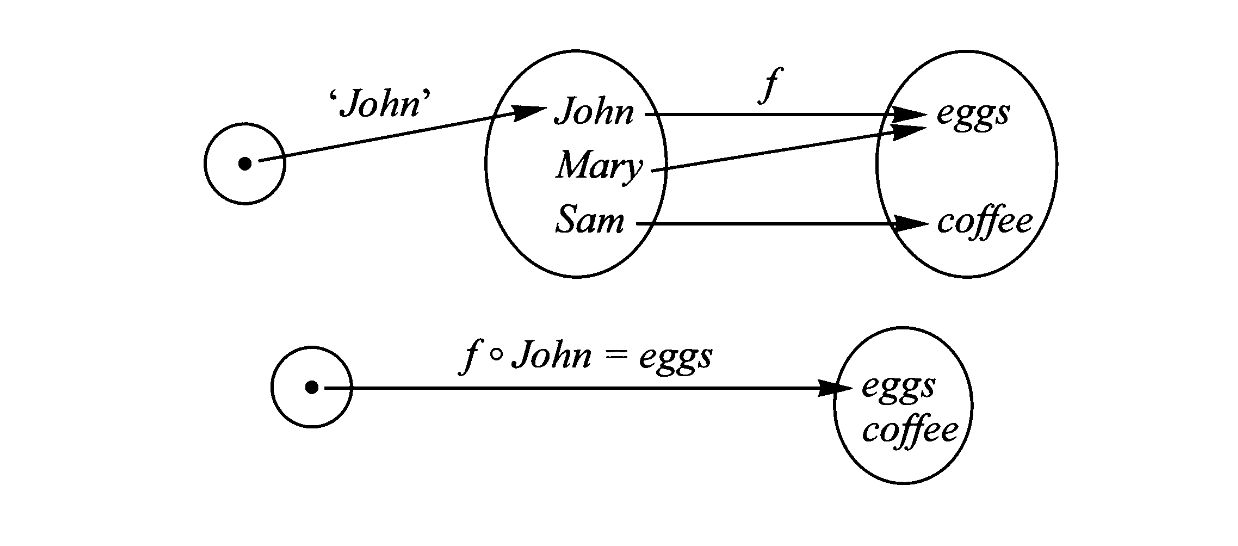
这个映射将集合的元素
和映射 等同起来。它可以理解为我们从集合中选取一个元素,而这个选取映射由于只选取一个元素,那么选取这个操作就和被选取的元素等同起来。这样做的好处在于,我们可以把 视为 ,于是 ,因此根据映射的复合,任何一个复合映射的像元素 ,都可以看成是一个复合映射 。
第二讲
- 关于映射,我们真正在乎的是输入和输出,而非任何中间过程,这就是为什么在映射的定义中只有关于输入和输出的抽象。比如考虑两个映射
。这两个映射的规则不同,但他们最终的结果是相同的,我们不是在规则本身的意义上说两个映射相同,而是在规则所实现的意义上说二者是相等的。 - 映射复合中,映射作用的顺序与书写顺序正好相反。例如
。 - 映射的复合可以类比为做流水任务,流水线的顺序很重要(因此映射的复合没有交换律),但流水线中哪些任务可以打包成一个任务不重要(映射复合的结合律)
- 映射的复合是凝缩,它把中间的历史省略,只保留初始和终止的状态信息(中间域的信息完全丢失)。
- 同一个映射可能被拆解为若干种复合方式。
- 外部图示忽略映射的规则,只考虑定义域和陪域
- 关于映射的数量。在有限集合范畴中,定义域和陪域都是有限集,因此给定二者,可能的映射总共有
个。特别的,当 时,存在一个空映射。而当 时,我们规定没有映射存在。若当二者均为空集时,也规定存在一个空映射。
第三讲
关于幂等函数即
第二部分、复合的代数
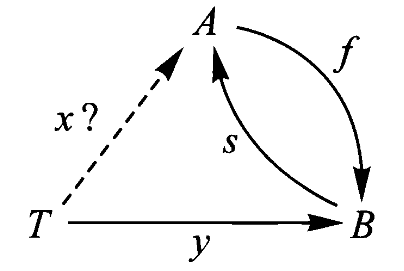
我们考虑如下类比:如果映射的复合像数的乘法,那么什么像数的除法?对该问题的答案延伸出大量不同问题。
第二篇、同构(isomorphisms):收缩,截面,幂等,自同构
1、同构
我们仍旧拿有限集合范畴举例。我们回忆所谓的“数”是怎样被定义的,犹记得小学课本中学习数字的时候,课本上通常画着三个香蕉、五个苹果这样的东西。但是从具体的三个香蕉、五个苹果中抽象出三、五这些数字,并不是一件简单的事。譬如在亚马孙雨林中的一些原始部落,他们的语言中缺乏数字概念。数字概念的诞生需要语言本身的抽象能力,而这种抽象能力则是社会实践所要求的。
数是抽掉了一切具体特征的纯粹量。数学课本其实已经帮我们做了这一步,书上画的是三个香蕉,而不是两个香蕉+一个苹果,因为前者更容易被视为一个可计数的整体(可加的整体,或单位相同)。但是即便三个都是香蕉,我们也抽象掉了香蕉的品种、颜色、尺寸等等差异,当我们把这些东西归为一类并用数计量时,背后隐藏的假设是它们是可通约的。比方说如果还是两个香蕉+一个苹果,我们就可以说它们是三个水果,苹果和香蕉之间的差异用一个更广大的概念水果囊括了。这种抽象到极致就是“东西”,如果我们把任意的东西放在一起计数,那种能够抽象掉东西之间所有差异性的概念,就是纯粹的量。
因此,计数的前提是抽象掉差异。而当我们把这些东西放在一起计数时,集合的概念就已经出现了。因为只有它们首先构成一个集合,在知觉层面被统合为一个可被计数的整体,它们才能被计数。随之而来的等量,则就是用量上的对应去抹杀质的差异。
例如,下面的映射揭示出某种相似关系(resemblance)。其中母亲对应于羽毛,父亲对应于石头,孩子对应于花朵。当然你可以从拟人的修辞手法出发,把这种对应关系解释为于母亲的形象是温柔,对应于轻软的羽毛,坚毅的父亲像石头,孩子像成长的花朵。但是从数学的纯粹的量关系出发,这种对应是任意的(arbitrary),母亲对应于羽毛完全仅仅是因为母亲作为一个元素在集合
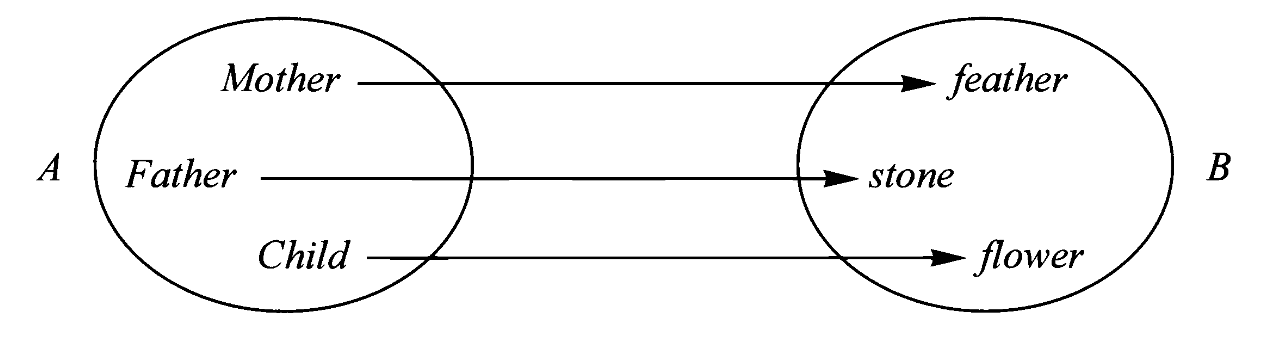
一切能和
我们把这种相似关系抽象出来,形成同构(isomorphism)的定义:一个映射
我们需要注意到,逆映射和同构映射是一套伴随概念。即一个映射能成为同构,必然存在其逆映射,而其逆映射本身也相应的成为一个同构映射。
对象间的同构关系具有下列性质:
- 自反性(恒等映射是同构映射)
- 对称性(同构映射的逆映射也是同构映射)
- 传递性(同构映射的复合也是同构映射,特别的同构映射复合的逆,是同构映射的逆的复合
)
也许你觉得这些到此这些东西都是大惊小怪,毕竟作为例子的三元集合之间的等价性实在太过显然。那么不妨考虑历史上笛卡尔的思辨,他的解析几何开创于下面这个同构:
其中左侧是欧氏几何平面,而右侧是二元实数组。通过系统性的运用这一同构,笛卡尔得以将困难的几何问题转变为简单的代数问题。
关于逆映射还有一些零散的说明。首先同构映射的逆映射是唯一的。
证明:假设
都是 的逆映射,那么 。于是 。
其次,既然我们将映射的复合与数的乘法相类比,那么逆映射就和乘法的逆运算相类比。但我们需要注意的是,由于乘法满足交换律,在定义乘法的逆元时,我们只需要单边乘法,例如
而当我们在映射语境下讨论除法的类比时候,逆映射也会派上用场。此外,除了这样标准定义的双边逆,还有所谓的单边逆,即左逆或右逆。
取消律:若
- 若
,则 。 - 若
,则 。
该命题不成立:若
为证伪这个命题,找到反例
即可。考虑一个二元集合 上的自同态。我们将证明即便考虑 有逆的情况,这个命题也不成立。 上的可逆映射只有两个,一个是恒等映射,另一个是交换两个元素的映射 。前者不足以证伪,取后者。然后取 ,即可。
2、一般除法(division)问题:决定(determination)和选择(choice)
数的除法问题是乘法的逆问题,即给定一已知乘数与积,如何求另一未知乘数,使其与已知乘数的乘积为已知积,写作方程为
- 决定(determination)或延拓(extension)问题:给定
,求 使得 。图示为
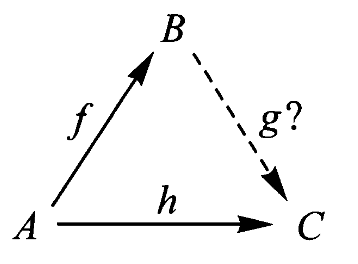
- 选择(choice)或提升(lifting)问题:给定
,求 使得 。图示为
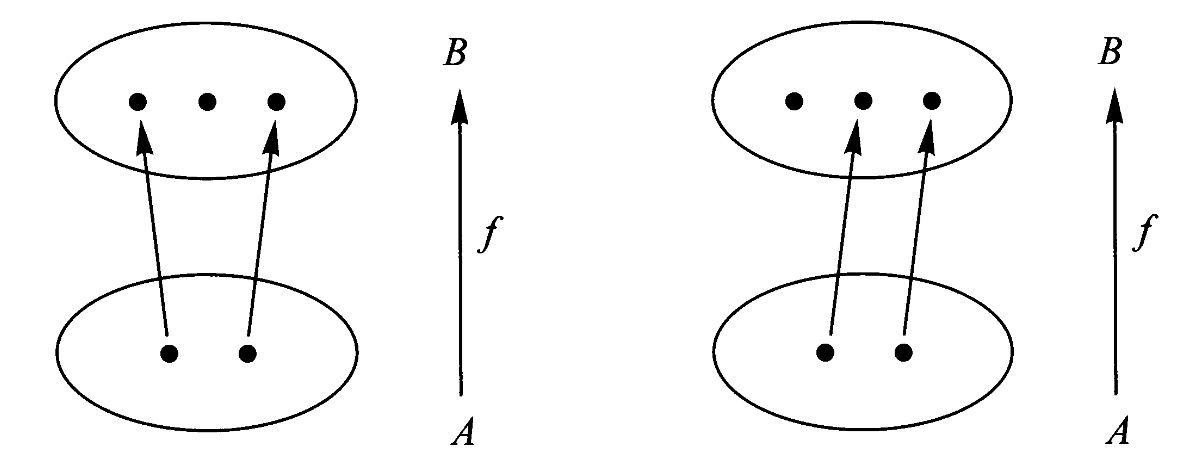
决定问题的例子:
如果
选择问题的例子:
考虑
那么我们可以找到多少
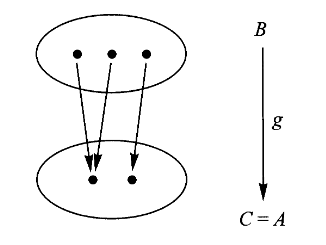
关于选择和决定这两个术语的直观理解。由于我们知道映射的特点是定义域里一个点映射且只能映射到到陪域里的一个点,因此对于有限集合范畴而言,选择问题已知
求 ,对任意 那么 需要把陪域中点 在 中的原像 中的点映射到在 中的原像 中的点,也就是说每给一个 ,为它选择一个 。如果原像非空,这样的选择一定是可行的。反过来选择问题无解的情况就是存在一个 , 但 ,也就是要把一个非空集合的元素映射到空集,这违反了映射的存在性。 而对于决定问题而言,已知
求 ,由于对任意 ,已经有了 ,因此 已经被决定了,它必须把 映射到 。反过来决定问题无解的情况就是存在 但 。也就是说在 中的唯一值 却被双重决定了,这违反了映射的唯一性。
关于决定的例子:伽利略的比萨斜塔实验证明了(在无视空气阻力的条件下)自由落体的距离被时间决定,在此以前人们以为下落距离与物体质量有关。这一发现用图示表明为
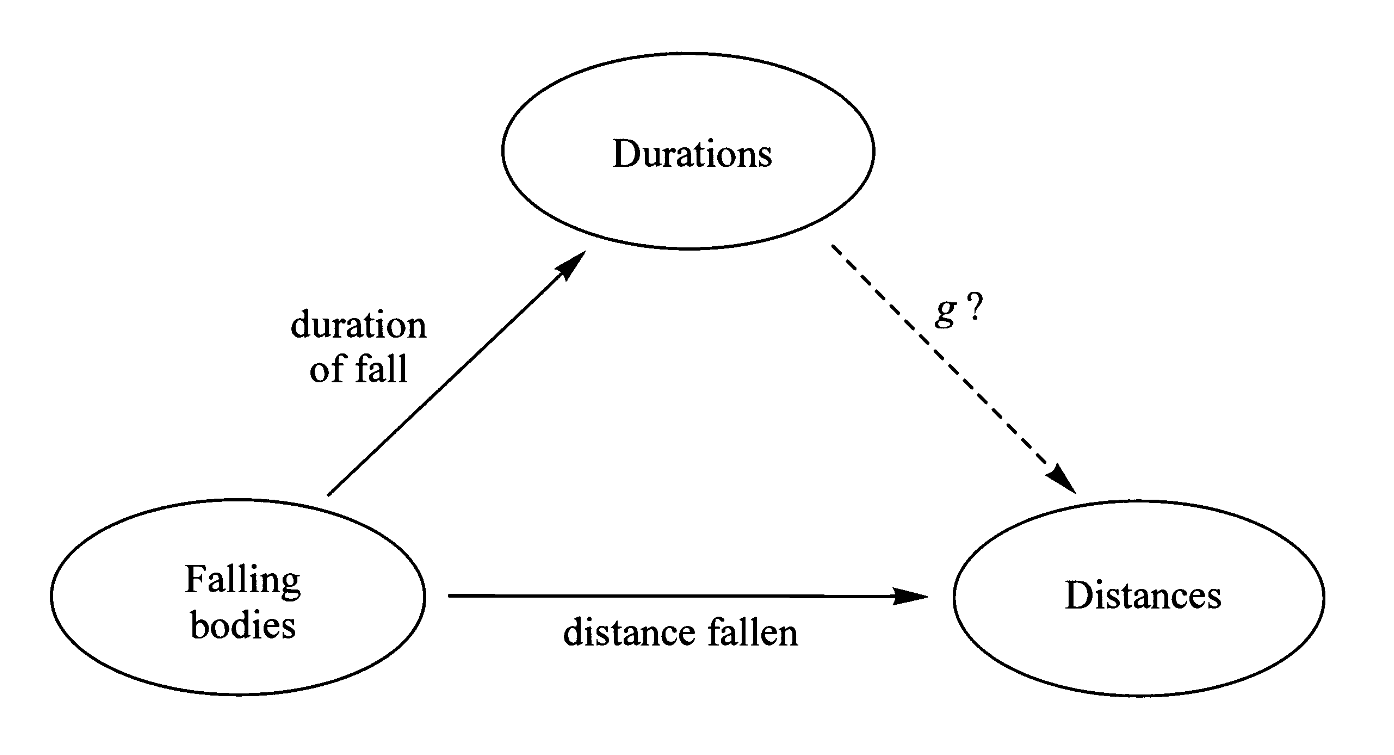
也就是说原本落体的下落距离可能是一个较为复杂的映射,需要考虑落体自身的各种性质(比如颜色、质量、形状、大小),然而现在通过发现这一决定性的因素,映射被压缩到唯一的性质即下落时间上。于是我们可以研究自由落体的运动规律,而这一规律由
3、收缩,截面,幂等
在决定和选择问题中,若
定义:若
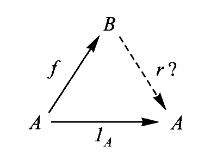
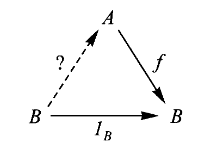
简记为
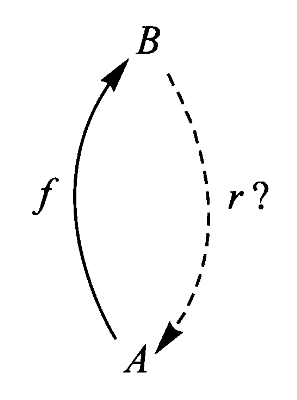
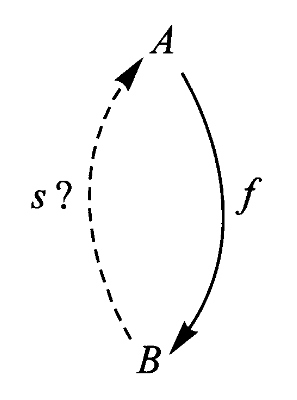
不过我们以上这种简记有一点不如三角形图示,三角形图示提醒我们我们所要求的映射必须是三角形“交换”,也就是说必须找到这样的映射使得三角形图示中的两条路径等价(可交换),而且这个简记图示容易忽略恒等映射究竟是关于哪个对象的。
注意收缩和截面在定义上的对偶性。也就是说,如果
是 的收缩,即满足 ,那么 就是 的截面 ,反之亦如是。
关于这两个名称的由来:所谓收缩其实源于拓扑学中的收缩,对于
,称 收缩于 ,若存在一个映射 ,满足 。也就是说对 中本身的点收缩映射是恒等映射,而收缩映射把 收缩到它的子集 上。因此, 是自然嵌入 的左逆,即 。反过来可以把自然嵌入看成是 在 上的一个截面,当然一般的截面未必是自然嵌入,而是说 中的每一点都可以在 中找到唯一的一点与其对应,就好像在 中截出了 ,即与 一一对应的像 。
此外我们还可以知道,构成三角交换图的收缩映射一定是满射,这是因为对任意
, ;截面一定是单射,这是因为若 ,设 ,则 。
由上一节选择问题的例子可知,如果某个映射存在截面,那么这种截面可能有多个,同理某个映射也有可能有很多收缩。有些映射可能只有收缩没有截面,有些只有截面没有收缩,有些则两者都没有。我们可以通过映射本身是否满足一些必要条件来断定其是否存在收缩或截面。
命题 1:若
证明:记
注意到命题 1 可以类比数乘法中的乘法逆元,如果
如果有映射
事实上这一通俗理解其实相当于命题 1 的逆否命题,即若存在一个对象
和一个映射 ,使得对所有映射 ,都有 ,那么映射 没有截面。特别的,我们说一个选区没有居民,就是说存在对象 是一个单元素集,映射 指找到 中的那个没有居民的选区 ,即 。那么对于任何映射 指从全体美国公民中找到一个人 , 就意味着 , 居住在选区 ,然而这是不可能的,因为选区 没有任何居民。因此逆否命题的前提成立,结论就是 没有截面,也就是不存在为每个选区 ,找到一个代表 代表 , 。 而我们说一个选区没有居民,其实就是在说 不是满射。
由于收缩和截面的对偶性,我们有下面这个对偶命题:
命题 1*:若
证明: 设
命题 2(左消去律):若
证明:设
相应的,我们有对偶命题:
命题 2*(右消去律):若
证明:设
类比数的乘法,我们可以发现命题 2 是映射复合的消去律。其中数的乘法消去律的前提是被消去元本身有逆,而此处映射复合的消去律也需要被消去映射的可逆性(注意一个映射存在收缩映射相当于存在左逆,而一个映射存在截面映射则相当于存在右逆)。
定义:满足左消去律的映射被称为单射 injective 或 单态射 monomorphism,满足右消去律的映射被称为满射 surjective 或 满态射 epimorphism。
注意左右消去律对任意对象
都成立,如果这里的对象不是任意的,那么还有个次一等的概念叫对从 出发的映射是单射/满射,这个概念是带限定词的。
在映射的语境下我们将单射或满射,但在态射的语境下我们将单态射或满态射。二者的区别我们可以大致这样划分,前者是一般的函数语境,对单射或满射的判定依赖于原像与像的关系,是元素层面的,即单射是相同像元素必有相同原像,而满射是任一值域元素都有原像。而后者是更普遍的范畴论语境,即对单态射或满态射的判定则依赖于映射复合层面的,即映射的左消去律或右消去律。当然特别的,如果我们考虑单元集映射作为满足消去律的一个特殊映射,那么单射与满射都可以视为是单态射与满态射的一个特殊情形。
补充:
还需要注意的是,命题 1、2 都是充要条件,也就是说当结论和前提是等价的。 命题 1 的逆命题:若对任意对象
证明:由于前提中对象与映射的任意性,取
命题 1 *的逆命题:若对任意对象
证明:由于前提中对象与映射的任意性,取
命题 2 的逆命题:给定
证明:由前提中对象与映射的任意性,取单元集
命题 2 *的逆命题:给定
证明:反证法。因为命题 1 是充要的,那么命题 1 的否命题也成立。我们假设
这个证明略显繁琐,主要宗旨是通过证明
不是满射,构造出两个在 值域外不同的映射,从而归谬。
综上所述,我们列出以下命题:
有收缩映射 有左逆 是分裂单态射 split monomorphism 满足左消去律(命题 2 的结论) 是单态射 是单射 满足命题 1 的结论
对偶的,我们有以下命题:
有截面映射 有右逆 是分裂满态射 split epimorphism 满足右消去律(命题 2 *的结论) 是满态射 是满射 满足命题 1 *的结论
对所有范畴而言,其中
对具体范畴 concrete category——也就是能找到一个从范畴到集合范畴的忠实函子,或者说该范畴有一个底层集合范畴结构——而言,态射
图示如下
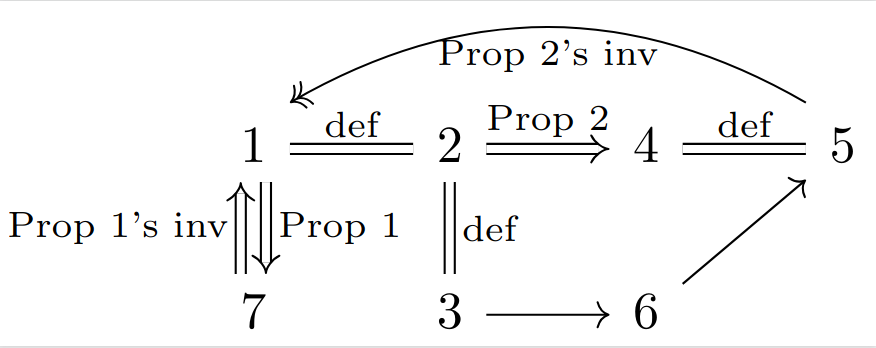
其中加粗箭头代表普遍成立,普通箭头代表对具体范畴成立,双箭头代表需要选择公理。
命题 3(收缩的复合是复合的收缩):若
证明:记
命题 3*(截面的复合是复合的截面):若
证明:记
定义:自映射 endomap
命题 4:若
如果我们把收缩和截面映射称为恒等映射的分裂因子,那么该命题可以总结为恒等映射分裂因子的反向复合是幂等映射。且恒等映射和幂等映射分别是收缩映射的定义域和陪域(截面映射的陪域和定义域)上的自映射。
证明:
命题 5(逆的唯一性): 若映射
证明:
这也就是说,如果某映射既左可逆又右可逆,那么它可逆且逆唯一。
4、同构 isomorphisms 和自同构 automorphisms
我们可以用截面和收缩的语言来重新叙述同构的定义。
定义:一个映射
命题 6:(同构的复合也是同构,且复合的逆是逆的复合)若
证明:显然。
求复合的逆相当于逆的反向复合,这可以直观理解为先穿袜子再穿鞋,先脱鞋再脱袜子。
对于有限集合范畴而言,对象间有同构映射意味着两个集合对象有相同数量的元素。同构给了我们另一个无需依赖计数的“数量相等”的定义,这对推广到无限集合尤为重要(即等势)。如果两个对象之间具有同构映射,那么我们就说这两个对象同构 isomorphic。集合范畴以外的范畴通常有结构更丰富的对象,在那里同构就不仅仅意味着元素数量相等,还意味着它们具有相同的形状、相同的结构等等。
那么,两个对象间有多少同构映射?这个问题立马导向另一个问题,对象到自身有多少同构映射?这种既是自态射又是同构的映射被称为自同构 automorphism。
一般而言,如果存在从
注意到
传统上,集合范畴的自同构称为置换 permutation,意味着它以特定的方式调换集合内的元素。这种变换带有简单而有趣的结构,于是我们可以借之描述第二个关于范畴的例子,置换范畴 the category of permutations。其中的一个对象是一个集合
映射的保持置换性可以直观理解为集合范畴上以下交换图成立:
置换范畴中映射的复合
除了是集合范畴映射的复合
我们将会看到置换范畴不仅有元素个数,还有轨道长度、重数等性质。而在这个范畴意义下的同构对象的这些性质将完全相同。
总结:略。该图已经被我们上一节的补充说明囊括了。我们来证注记中的命题。
命题 7:若
证明:设左逆为
命题 7*:若
证明:类似。
第四讲、映射的除法:同构
1、映射的除法与数的除法
若映射的复合类似于数的乘法,那数的除法类比是什么?
我们知道数的除法是数的乘法的逆运算,因此映射的除法也应该是映射的复合的某种逆过程。我们同样知道,这种逆过程的结果有可能不存在也可能不唯一。正如数的乘法问题中,存在两种特殊情况:
对数的乘法而言这是特殊情况,但对所谓的映射的复合而言这却是典型情况。不过我们可以先处理一种存在唯一解的简单情形。
2、逆和倒数
略。
注意若映射
3、作为除数的同构
看电影时,你可能要处理三种同构映射:
- 角色名与角色(搞清谁叫什么名字)
- 角色与演员(搞清谁演什么角色)
- 演员与演员名(搞清演员叫什么名字)
而在片尾角色表中则是这三个同构映射的复合,即角色名与演员名的映射。
尽管复杂,但你也不至于混淆,这都归功于同构的可逆性。事实上在搞清某个角色扮演者的名字的过程中,我们在处理这样的映射除法问题。
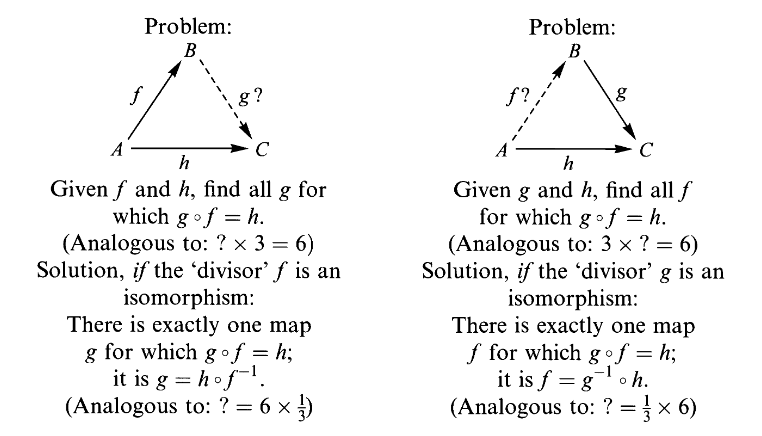
因为这些复合中涉及了同构映射,因此映射除法的解存在且唯一。
4、其他范畴中的同构一览
代数中我们常常遇见带有一些规则的集合,例如全体实数的加法群
这里是若干关于该范畴中映射的例子:
- 实数加法群自态射
。 - 实数乘法群自态射
。 - 实数加法群到正实数乘法群的态射
并且这些映射还都是同构,因为我们能找到其逆映射。
我们还知道两奇数相加为偶数,两偶数相加为偶数,一奇一偶相加为奇数,那么
如果你觉得这些例子中出现的代数规则还有些神秘,别担心你不是一个人。我们的目标之一就是通过找到其根源来祛除神秘。当我们找到、培植那根源,你就会惊讶于它的枝节伸出多远。不过先让我们暂时习惯于把这些代数规则当成例子的源头。余下的例子是几何的,不涉及严谨的代数运算。
在几何学中,”欧几里得范畴“占据了一个显要的地位。其中的对象是任何可以画在平面上的多边形,而从一个图形
在拓扑学中,映射不一定要保持距离,只需要连续,即如果
放射科医生在检查 X 射线拍摄的人体图像时,需要做出更清晰的区分,因此可能会使用更精细的范畴。其中的对象可能还每个点上附带一个密度函数,因此除了保持连续性之外,映射还必须具有这样的特性:如果 p 和 g 相邻,并且 p 处的密度大于 g 处的密度,那么相应地,fp 处的密度也大于 fg 处的密度。如果找不到从你的身体到”理想“身体的同构关系,就说明有问题。(不要把这个例子看得太严肃,它只是为了让你了解人们是如何通过设计适当的范畴来捕捉任何主题的重要方面)。
第五讲、映射的除法:截面和收缩
1、决定问题
许多科学研究都是从观察一个量
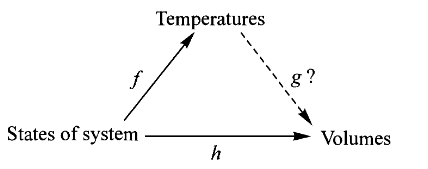
我们猜测,存在一个映射使得
注意,温度和体积本身都是气体系统的一个表观函数 observable function,因此当我们求
作为温度和体积间的函数关系时,其应满足的条件用映射复合的语言来描述是必要的,因为它不是两个直接量之间的函数,而是映射的映射,是把同一个系统状态经由两个不同的映射路径得到相同的表观量,即满足交换条件 ,如果把它仅仅视为两组表观量的对应,即对任意 ,满足 ,是不够的,因为这两组表观量并没有揭示它们源自同一个系统——也就是说 对条件的满足必须根据一个相同的系统,这就不得不引入映射的复合,即范畴的语言。此外查理定律成立还有一个前提,即系统的压强恒定——这在图中是隐含条件。
另外,尽管我们在数学上将其称之为决定问题,但它并不是那种单一意义上的决定。理想气体的诸多表观量其实是相互约束的,或者说是多元决定的。所以尽管我们说温度决定体积,但决不能忘记是在压强恒定的前提下,显然正是因为压强本身也在决定体积,所以才需要固定之。因此当我们说某量决定另一量时,我们必须明白它未必是唯一的决定因素。
再举一个关于决定问题的反例。如果我假设班上同学是否戴帽子被其性别决定,实际上就是希望找到这样的映射
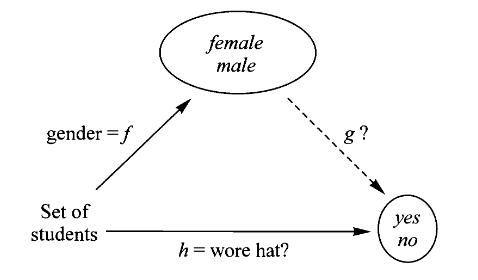
显然这意味着只有两种可能:要么所有男生都戴帽子或都没戴帽子,要么所有女生都戴帽子或都没戴帽子。只要有一个男生/女生戴帽子,另一个男生/女生没戴帽子,这种映射就不存在。也就是说,决定映射是一种收缩,相同性别的人必须也有相同的行为。反过来,只要找到两个学生,他们性别相同但行为不同就能证明决定问题无解。形式上,若决定问题有解
2、一个特例:常数映射 constant maps
现在考虑
定义:映射值唯一的映射称为常数映射,或等价的可以被单点集分解 can be factored through 1 的映射称为常数映射。
3、选择问题
练习 2a:显然。
逆命题也成立(练习 2b),它是命题 1 逆命题的推广(前提比其更弱,即
证明:由
4、除法的两种特例:截面和收缩
略。注意截面和收缩总是相对于某一映射而言,它是两个映射之间的相互关系。永远不要单独问某映射是否为截面或收缩,那是没有意义的。
5、堆叠 stacking 或分拣 sorting
为了找到某个映射
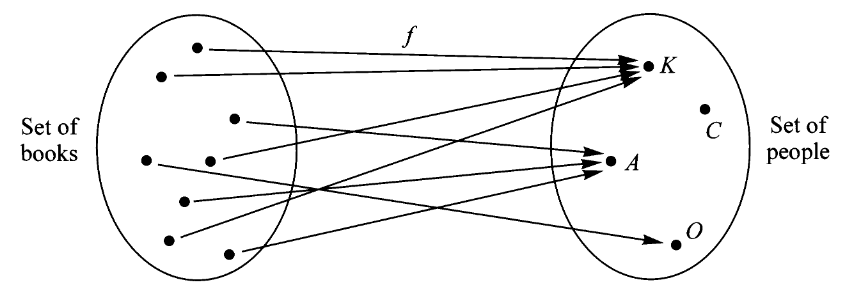
我们可以把这种图示画成更整齐的形式
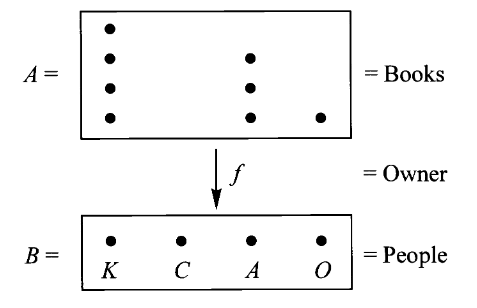
其中,每个人排成一行,属于同一个人的每本书排成一列。
实际上,这张图可以这样画,首先枚举陪域中的全部元素
排成一行,然后考虑每个元素的原像 ,将其中的元素 排成一列即可。
为了找到其截面映射,我们只需考虑为每个
6、中餐馆中的堆叠
想象我们在参加完一场数学研讨班后前往中餐馆吃饭。在餐馆中,把盘子按形状堆叠在一起能够有效计算账单。
餐馆中的一个基本映射是菜单
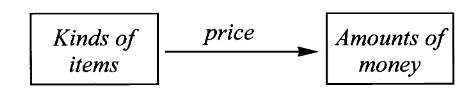
它把每道菜品映射为价格。
每桌顾客就餐对应的映射则是每份菜所属的品种。
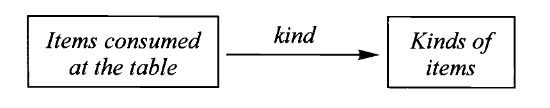
这个映射是既不是单射也不是满射,因为有可能一道菜点了好几份(非单射),同样的不可能每道菜都点了一份(非满射)。
因此,结账时计算总价的方法则是计算桌上每份菜的价格并求和,即考虑以下复合映射并求和
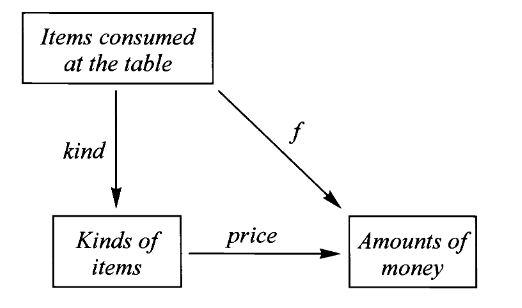
总价为
品种
价格为
但在这家特殊的中餐馆,这个映射无需纸笔而用物理形式直接记录,即堆叠餐盘。把餐盘形状和菜品价格对应起来的映射
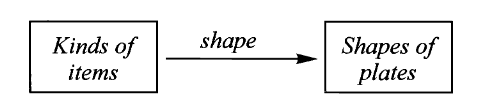
其中同一价格的菜品必须用同一种形状的餐盘盛放,换言之餐盘形状唯一的决定了所盛放的菜品的价格,即满足交换图
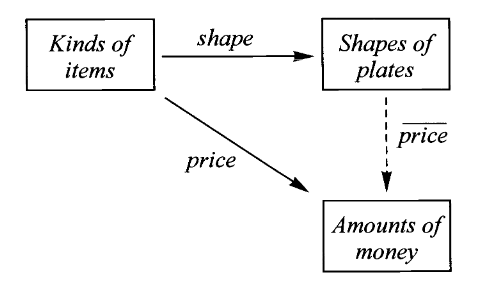
因此收银员只需要知道餐盘形状对应价格的映射
用餐完毕后,空盘子按照形状堆起来
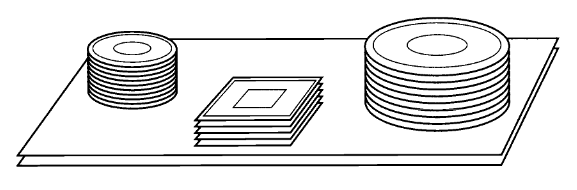
这个映射是
这个映射是特定顾客点了特定菜的结果,它可以与
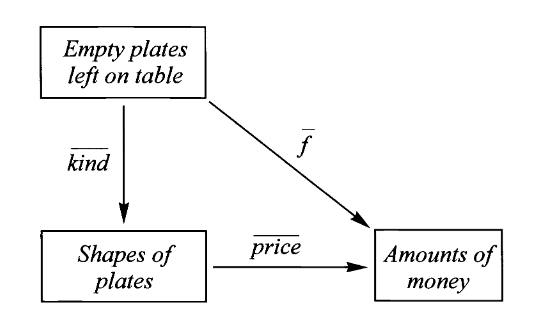
只需看一眼桌上餐碟的摆放,收银员就可快速计算出账单
为了证明这种计算方法和上述的计算方法是一致的,只需要证明对相同价格
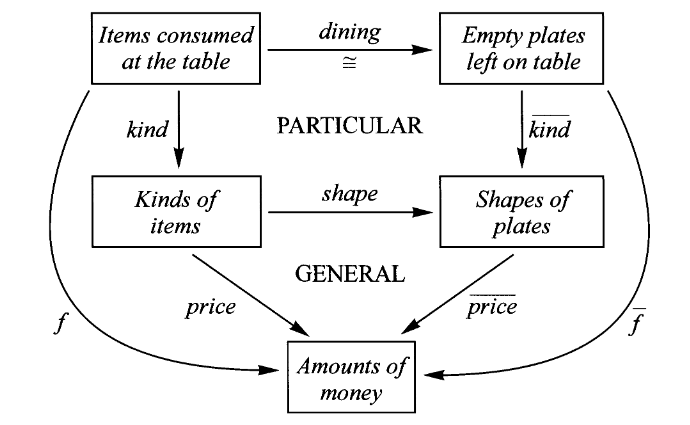
其中
所谓堆叠数目相同其实就是在说,
。
在这个交换图的上半部分,是不同顾客点不同菜的特殊性;而在下半部分则是菜品、餐具、金额的普遍性。只要菜品不更新、菜价不上涨、餐盘形状不变化,无论顾客口味如何、消费如何都不会影响交换图下半部分的计算。同时通过这种分解,收银员不需要追溯顾客具体点的菜品,只需要专注于影响价格的普遍性因素(餐盘),而因为餐盘本身在用餐过程中保持不变,也就将具体的菜品与价格计算隔离开来。
第六讲、映射的两个一般视角或用途
1、将定义域按属性分拣 sorting of the domain by a property
我们可以把映射视为对定义域的某种分拣 sorting,事实上可以把陪域中的每个值看成是定义域中元素的属性值,然后按照相同属性值把定义域中的元素分拣为不同堆叠 (stacks/sorts),本质上就是用原像来分割定义域,即
我们也可以用纤维化 fibering 描述这种视角,我们说
分拣可以进一步被分拣。例如所有生物可以归为不同种,种又可以归为不同属。从纤维化的角度来看,我们首先得到第一层纤维束,然后又把纤维束两两束缚成更大的纤维束(类似于肌肉的构造)。
2、对陪域命名或采样 naming or sampling of the codomain
我们还可以把映射视为对陪域元素的命名或采样,事实上可以把陪域中的每个值看成是被定义域所参数化,即
3、两种视角的哲学解释
我们可以从哲学方面来解释映射的这两种视角。现实由鱼、河流、房屋、工厂、田野、云朵、星星,即运动和发展中的事物组成。现实还有一个特殊的部分:例如,文字、讨论、笔记本、语言、大脑、计算机、书籍、电视,它们在运动和互动中都是现实的一部分,但又与现实有着特殊的关系,即反映现实。
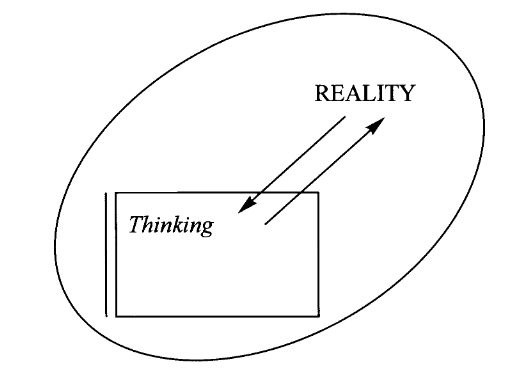
所谓思维就是观察、操作、感知、思考。这种反思过程的结果就是知识,而积累的知识及其内在关系的整体就是科学(其目的之一是计划对现实的进一步操纵)。科学实际上是相互关联的科学综合体,关注现实的不同方面。哲学是其中一门特殊的科学,它(作为常识)反映了现实中的这种特殊关系,即思维与现实之间的关系。因此,在所有科学思维的复合体中,存在着客观与主观之间的特殊关系。
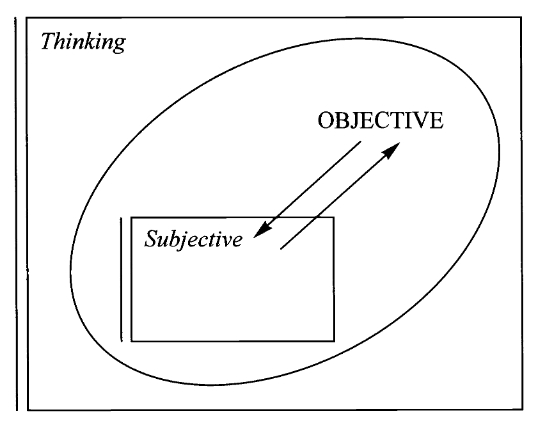
在客观方面,我们努力尽可能清晰地描绘现实,因为它本身就是现实,并且在现实中运动,与我们的特定思想无关;在主观方面,我们努力尽可能清楚地了解思维(如上所述)本身的规律,从而得出语法、纯粹逻辑、代数等方面的规律。
当我们在某个给定的客观范畴(如集合范畴)中选择一些对象
简而言之,我们用各种各样的抽象对象
去研究现实事物 的不同方面,把现实事物在不同方面呈现出的性质、结构表示为其与这些抽象对象之间的映射 ,这样这些映射本身就记录着我们关于 的知识。
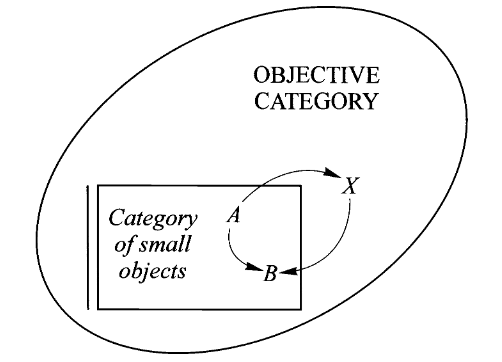
通过把具体对象分解为更小的对象,我们上述考虑一个映射的两种方式就不再仅仅是两种态度,而是有实际的差异:定义域更小的映射(列举 listing)与陪域更小的映射(性质 property)。
第七讲、同构和坐标
1、同构的用处之一:坐标系
如果命名映射是同构的,上一讲讨论的主观蕴含于客观之中,或者说熟悉蕴含于一般之中的思想就特别容易理解。也就是说,如果我们掌握了从已知对象
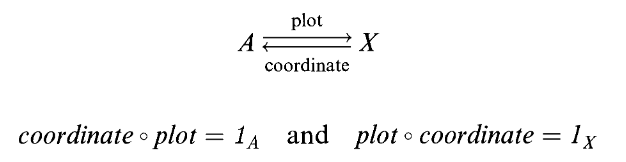
例如从实数到直线的映射,我们只需确定原点、单位长度、正方向这三个要素就可以确定一个标准的实直线映射
以实数集
回到几何学。笛卡尔的解析几何就是用
再举一个非实数的例子。考虑淘汰赛,假设有八名参赛选手,主办方需要按照选手的世界排名排序确定赛程,例如

一旦确定了种子序号,它们便会按照以下赛制进行淘汰直到角逐出冠军。
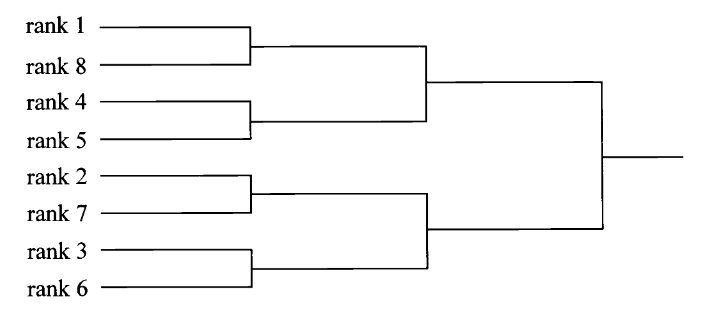
我们知道下方这张图是普遍的,它适用于任何八人淘汰赛,而上方的同构映射是特殊的,因为每次比赛的参赛选手可能不是相同的八个人。
一旦我们确定了这种同构关系,我们就会习惯性的用
2、同构的两种滥用
第一种滥用是当我们假定
第二种滥用则是当我们假定
总之这两种滥用都与对象上的额外结构有关,在讨论同构时我们必须明确它保持哪些结构又忽视哪些结构,总之必须明确同构作为一种映射,需要在一个特定的范畴意义下考虑。而这种滥用只会在抽象情况下发生,你可能会把 1 和 8 相加,但当你明确 1 和 8 是选手的种子号以后,你就会意识到把 1 号选手和 8 号选手相加并不能得出任何有意义的结论。
第八讲、表现映射特征的图像
略
第九讲、收缩和幂等
1、收缩和比较
我们用
定义:
记号
不是标准的,仅限本讲使用。
命题: 关系
证明:显然。
2、幂等是收缩的记录
我们知道,给定一对收缩和截面映射
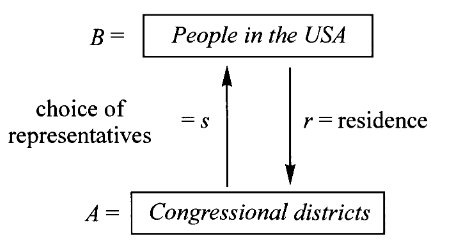
根据选举法,每个选区的代表必须该区居民
这个不动点集合与所有选区集合是同构的,因为每个选区会选出一个代表。
再看看幂等映射的内部表示。对于
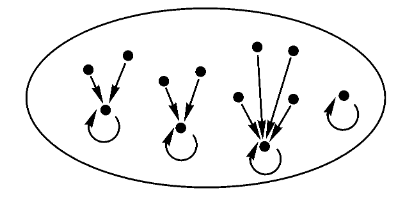
尽管我们不知道原来的
定义:若
上面这样构造出来的
就是 的一个分裂。但是这样的构造仅限于有限集合。不过这个定义却是一般的。
我们接下来证明,
命题:若
证明:令
又
故这样构造的
因此,根据这个可分性定理
算术中的例子:如果
3、困惑
我们看到上面这个例子,是试图用对象
总之,即便
所谓数目更多但结构更简单可以这样理解,例如理想气体分子之间没有相互作用,而统计态的数目更多,但液体或者固体的统计态数目更少,分子之间的相互作用即结构却更为复杂。
4、三种收缩问题
略
5、比较无穷集
第 1 节中我们引入了
问题
举一个有收缩但没有截面的映射
的例子。 思路:如果
有收缩就意味着 是那个收缩的截面映射,因此对象 小于对象 。考虑 。显然 是一个收缩。但是不存在截面 使得 ,这是因为 不是满射。 若
,满足 ,是否可以证明 为幂等? 为幂等? 证明:显然。
是否可以根据 2 中的
导出映射 满足 ? 解:令
。 对问题 1 举一个无限集合的例子。
思路:我们只需要找一个单射非满射即可,例如
。首先 有收缩 。其次 无截面,因为 。
第十讲、Brouwer 定理
1、球体,球面,不动点和收缩映射
Brouwer 不动点定理:
设
为包含两端点的线段(闭区间), 为 的连续自态射。则该映射必然有一个不动点 满足 。 例子:设
是一段时间, 是一段从 到 的道路。假设有两辆汽车在这条路上行驶。第一辆车以恒定的速度从 开往 ,因此它的运动可以用 ( 表示匀速运动)来描述。与此同时,第二辆汽车沿着这条路的任何地方出发,漫无目的地向前行驶,也许偶尔会停一会儿,然后重走一段路,并在沿路的任何地方结束行程。用 表示第二辆车的运动。现在 是一个可逆映射,所以我们得到 ,令 为复合 。不动点定理告诉我们,在 中一定存在某个时刻 满足 。也就是说, ,故 ,这说明存在某个时刻,两辆车在路上的相遇。直觉上不难理解,如果第一辆车从起点开往终点,而第二辆车在此期间一直在两点之间行驶,那么第一辆车必然会在中途与第二辆车相遇。 设
为一个闭圆盘, 是 上的连续自态射,则 有不动点。 例子:旋转圆盘的映射是一个连续自态射。圆心是它的一个不动点。
设
为一个闭球体, 是 上的连续自态射,则 有不动点。
Brouwer 收缩定理:
- 考虑内射
将区间 的端点 嵌入区间。那么不存在 的连续收缩,即不存在连续映射 使得 。 - 考虑内射
将圆盘 的边界 嵌入圆盘。那么不存在 的连续收缩。 - 考虑内射
将圆盘 的边界 嵌入圆盘。那么不存在 的连续收缩。
事实上不动点定理的三种情况与收缩定理的三种情况两两等价。我们来证明收缩定理 2 能推出不动点定理 2。不过 Brouwer 证明的是它的逆否命题,即给定一个圆盘上的无不动点的连续自态射,可以构造出一个从圆盘到其边界的连续收缩映射。
2、逆否命题与原命题的等价性
3、Brouwer 的证明
假设
4、不动点定理与收缩定理的联系
命题 1:令
证明:反证法。假设这样的
需要注意的是,条件中
的连续性不可或缺,它是构造出连续 的充分条件。
命题 2:设
证明:对任意
命题 3:从不动点定理推导收缩定理。
证明:反证法。若收缩定理不成立,即存在
事实上通过命题 2 我们可以得出比收缩定理更强的结论,即不存在从
5、如何理解证明:概念的对象化和映射化 The objectification and mapification of concepts
你可能认为上述我们关于 Brouwer 定理的推理并不成立,毕竟我们连连续映射的精确定义都未给出。下面我们将提取出推理所需要的那些性质,并证明我们的结论在这些性质成立的任何范畴中都有效。
在它的证明中,除了球体
中的箭头 arrows 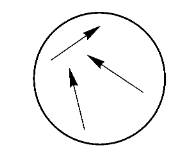
每个箭头在
中有一个头 head 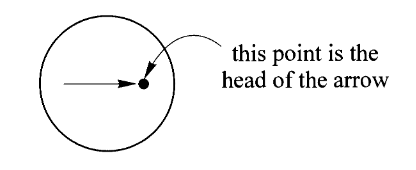
每个箭头在
中指向 上的一个点 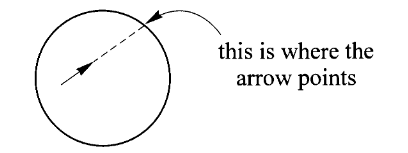
为了分析其证明,我们需要把这三个概念加入我们的范畴
- 一个对象
,其中的点是 中的箭头 - 一个映射
,为每个箭头分配其头 - 一个映射
,映射到每个箭头指向的点
这里使用“加入”
的说法,意味着 本身还是集合范畴?特别的它包含 。那么在此之前,是否还得证明它们构成一个范畴?还是说它们仍旧是集合范畴,只是比最小的那个集合范畴还多了一些额外结构。
而这个
如果
还是集合范畴,那么其中的映射似乎并不能直接称为连续映射,总感觉还是少了点什么。
于是我们有三个对象和三个映射:
我们要问这些(被对象化的)概念中的哪些特殊性质是在其证明中使用到的?
首先,我们看到如果某个箭头的头位于边界上,那么它的头就是它指向的地方,即
公理 1:若
如果一个箭头
在 中的头 恰好是边界上的点(通过内射 映射到边界上) ,那么它指向的点 就是这个头 。
我们的观察是针对一个箭头
从公理 1,我们可以得到 Brouwer 的部分论证:
定理 1:若
证明:令
推论:若
这里映射
是把 中的一个点映射为 中的一个箭头(即有序点对)。这应该正是指 Brouwer 证明中的把 映射为 , 为 上的自态射。
其次,我们还注意到如果
公理 2:若
要么两个点相同,要么不同就对应于一个箭头。
这样我们就能完成其论证:
定理 2:假设我们有映射
证明:取公理 2 中的
若取
若
这就是 Brouwer 定理。因为这个定理的前提是
看起来前面那个复杂的不动点证明就这样被神奇的证明了。其实我们这里所做的,不过是用范畴化的语言描述了抽象范畴中一般的不动点定理成立所需的两个公理。而具体的 Brouwer 不动点的证明实际上就是在证明公理 1 和公理 2 的成立。
因此我们前面做的繁琐工作并不是无用功,因为本身连续映射的复合仍然连续这个性质本身是我们所探讨的对象仍然构成一个范畴的基石。而且,我们恰恰需要把映射限制在连续映射的范畴中,才能证明子句 2 不成立。如果对一般的不连续映射而言,它们有可能满足子句 2 而不满足子句 1,也有可能满足子句 1 而不满足子句 2。
我们稍后会看到在许多范畴
这句话的意思是说,即便可能有时不存在
,但这里我们只需要存在 即可,也就是说在集合 中能取出点就够了。
总之我们关注的是如何通过将某些概念对象化为范畴中的映射,将概念的组合变为映射的复合!这样,我们就可以利用结合律把复杂的论证浓缩为简单的计算。早在几百年前,胡克、莱布尼茨和其他伟大的科学家就预见了具有这种特征的“哲学代数”的可能性。本节内容已经相当浓缩,要掌握它可能需要一些努力。你需要回到我们之前对布劳威尔证明的讨论,并将其与这一版本进行仔细比较。这样的研究会很有帮助,因为这个例子是范畴思维方法的典范。
6、暴风眼
设想一个流体在球形容器中运动(二维的例子是水在茶杯中旋转)。现在,球中的每个点都在移动,我们在该点上画一个带尾的箭头来表示它的速度。也就是说,箭头的长度与点的速度成正比,箭头指向移动的方向。是每个点都在以非零的速度运动呢,还是至少有一个瞬时的”暴风眼“?
要回答这个问题,我们需要一个与之前想象的略有不同的箭头对象 A。它的点是在我们的球中以非零速度运动的粒子的可能速度箭头。这些箭头的限制比我们之前的箭状物体要少,因为箭头的头部可以指向球外(它只是速度的表示,而不是球面上两点相连的表示);唯一的限制是,如果一个点在球的表面上,它的速度箭头就不能指向球外——起码与球相切(因为容器壁挡住了向外的法向速度分量)。
现在我们假设每个点都在移动,因此我们可以得到一个
公理 1 告诉我们如果流点
公理 2 告诉我们如果流体没有暴风眼,即流体内每个点
7、用映射来形式化猜想
我们回到不动点定理的一维例子。现在,我们假设道路并没有起点和终点,只是甲车从点
也就是在现在的问题情形中,放宽了道路的范围(道路
从有界放宽为无界)。但关键在于时间 本身,以及甲乙的起点与终点仍是有界的。
现在涉及三个对象:时间段
甲的行驶映射为
习题:
将甲乙的行驶限制用映射的复合表达。
参考 此处
由于现在道路是无界的,所以我们需要借助内射
利用 的有界性。这里内射的 指的是从 点匀速直线运动到 点的映射(即最初例子中的映射 )。这里行驶的起点和终点 是概念化的,它既可以指时间上的起点和终点 (因为甲乙是同时出发同时停止,因此时间上的起点和终点二者相同),也可以指空间上二者分别的起点和终点 。 那么甲的运动限制,即起点和终点恰好是
与 可以表达为 。而乙的运动限制则较为特殊,因为我们只知道它的起点 和终点 位于 之间,但是我们没有办法直接表达为它在 上的有界性。如果要用映射的语言来描述,我们必须借助 上的有界性,也就是借助内射 的逆映射(如果把它的陪域限制在 ,那么它实际上是同构),能够在时间段 上找到匀速直线运动恰巧经过 的时刻 ,也就是说存在 。因此关于乙的运动限制,我们可以表达为 ,满足 。 将甲乙两人在某时刻相遇的结论用映射的复合公式化(借助单元集
)。 存在
,满足 。 把例子中的
替换成 ,给出一个比 Brouwer 不动点定理更强版本的猜想。 令
为两个内射。给定映射 ,若其满足 ,那么存在 满足 。 给出猜想 c 的一个反例。
不会。