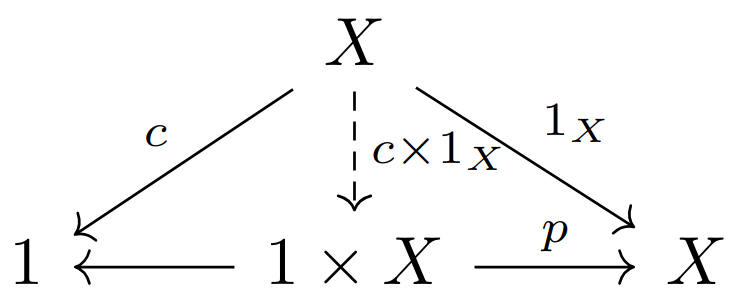我们将定义对任意范畴中的对象定义对象的积与对象的和。在不同的范畴中,加法和乘法之间的关系出奇地不同。
第四章、泛性质 universal mapping property
1、终对象 terminal object
在抽象集合范畴
所谓的泛性质从此得名,即某个特殊对象对所有对象都具有相同性质,这里的泛即普遍性,指的是某性质普遍的对所有对象均成立,而这种普遍成立的性质本身是特殊的。
定义:范畴
该定义通常被称为泛性质 universal property,因为它用与范畴
终对象有一个简单的例子,比如考虑任意有限全序集,其中的元素视为对象,序关系视为映射,则终对象就是极大元/极小元。
命题(终对象唯一性):若
证明:由于
这个命题的结论比同一范畴中的任何两个终对象都同构更强,因为这里的同构映射是唯一的。通常,两个同构对象之间可能会有许多同构映射,但终对象只有一个同构,因此终对象不仅仅在同构的意义下是唯一的,它根本就是唯一的(因为连那种同构关系本身都是唯一的)。只要某个性质可以用范畴的映射来表达,那么任何两个终对象都具有完全相同的该性质。因此我们总是取一个终对象并记为
即便终对象本身也不是完全平凡的,即使计算陪域为终对象的映射
定义:若
练习1:
解答:
练习2:在抽象集合范畴
解答:对于抽象集合范畴而言,我们已经见过点映射的定义,那就是从单元集
从此也可以看出终对象被习惯记为
的原因。
为证明单元集
练习3:在离散动力系统范畴中,对象的一点只是自态射的一个不动点(即动力系统的一个平衡态)。因此,大多数状态并不对应于来自终对象的任何
解答:这里对象的一点应该是指从离散动力系统范畴中的终对象到任意对象的一个映射,但我们往往直接把这个映射与它像点对应起来。这是因为我们已经知道如果一个对象在离散动力系统范畴中是终对象,那么它在集合范畴意义下也是终对象(因为任意一个集合范畴可以配上一个恒等自态射变成自态射范畴),即单元集,因此像也是单元集,即一点),因此我们要证明的是
练习4:在图范畴中,图
解答:这里的环指的是源节点和汇节点相同的箭头与该节点构成的图,不是由若干节点和箭头组成的大环。为证明这一点,先寻找图范畴中的终对象。我们证明,由一个节点和一个环箭头构成的图
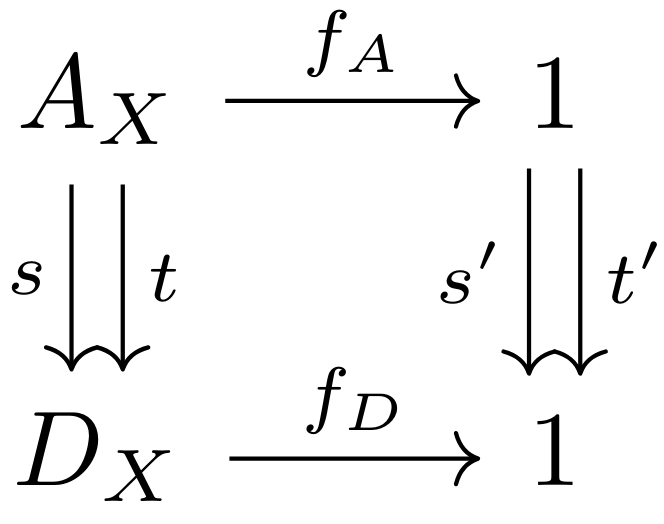
即
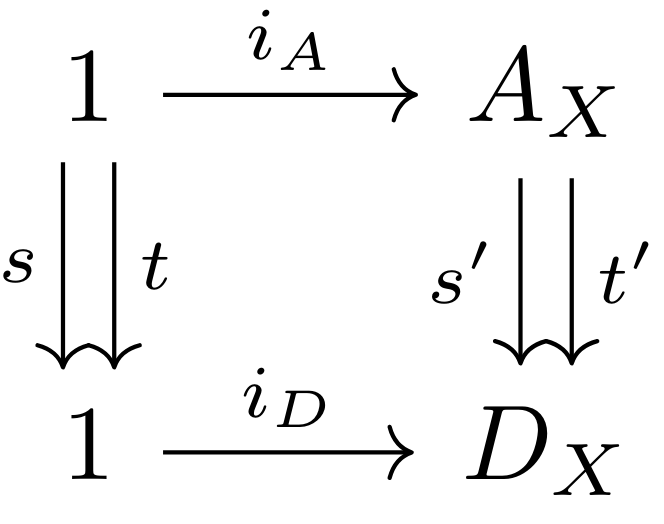
显然
练习5:集合范畴中的终对象
注意到该命题的逆命题显然正确。区分性就是
与 逐点成立的等价性, 因此即若找到一点 使得 ,则 ,即区分 只需要一个点 ;反过来如果 ,则必然能找到一点 区分它们 ,也即这种不同性是可以“实例化”的 。这与之前我们使用点映射作为探测范畴性质的方法相一贯。
解答:由练习2我们已经知道集合范畴的终对象就是单元集,而
自态射范畴中的反例,
其中
图范畴中的反例则可以再次利用上图,只需要把上面内部图示看成一个图即可。
由此我们注意到为什么可区分性在这两个范畴中不成立,这是因为在这两个范畴中,成为范畴映射的条件更苛刻了——相较于集合映射还要满足结构条件,因此点映射的范围缩小了,对每一个点映射有
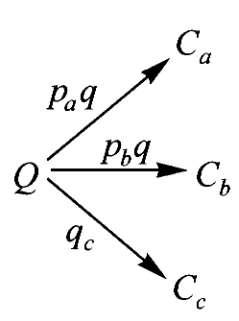
2、分离 separating
即使终图 terminal graph 不能分离任意两张图,由一些非终图可以做到这一点。考虑以下两张图
对任意图
若
对大多数我们给出的范畴例子而言,存在一些对象足以区分映射,即若
练习6:证明在离散动力系统范畴中,存在一个对象
解答:我们在会话十五第三节仔细讨论了自然数加法自态射集
3、始对象 initial object
范畴中许多关于对象或映射的一般定义都可以通过颠倒其中的箭头方向和复合顺序、交换定义域和陪域的地位而“对偶化” dualization。例如,与终对象相对应的对偶概念是始对象:
定义:范畴
练习7(始对象唯一性):若
证明:由于
习惯上我们记始对象为
练习8:在集合范畴、自态射范畴、图范畴中,若
证明:我们首先确定集合范畴中的始对象的具体形式。特别的,集合范畴中存在空集
随后考虑自态射范畴和图范畴,由于其中的映射首先至少是集合映射,而空集的自态射范畴和空图也都是其中的特殊对象,因此它们也是其中的始对象。而空映射显然满足保持结构的性质,因此也是相应的范畴映射。命题得证。
从此可以看出始对象被习惯记为
的原因。
练习9:定义带点集 pointed sets 范畴
证明:设
最后,练习8(b)的结论是对任意对象
这里我们滥用了记号,把点映射的字母和点映射的唯一像点字母等同起来。
这里之所以带点集中的始对象没有类似性质,是因为空集被排除了,这恰恰是带点集名义上的特点,即带点集必须至少带有一个点。
练习10:记
证明:由带点偶集范畴的定义可知,从这个始对象到任意对象的映射
练习11:证明在集合范畴中,若一个对象
证明:练习8中已经证明了,如果
至于自态射范畴练习8中也说明其始对象为空集的自态射,因此任何非空对象都不是始对象,而由练习3知道它的一个点是自态射的不动点,然而很容易找到不含不动点的非空自态射,例如
至于图范畴练习8中也说明其始对象为空图,因此任何非空图都不是始对象,而由练习4知道它的一个点是图中的环,然而很容易找到不含环的非空图,例如把前一个反例的自态射内部图示看成图。
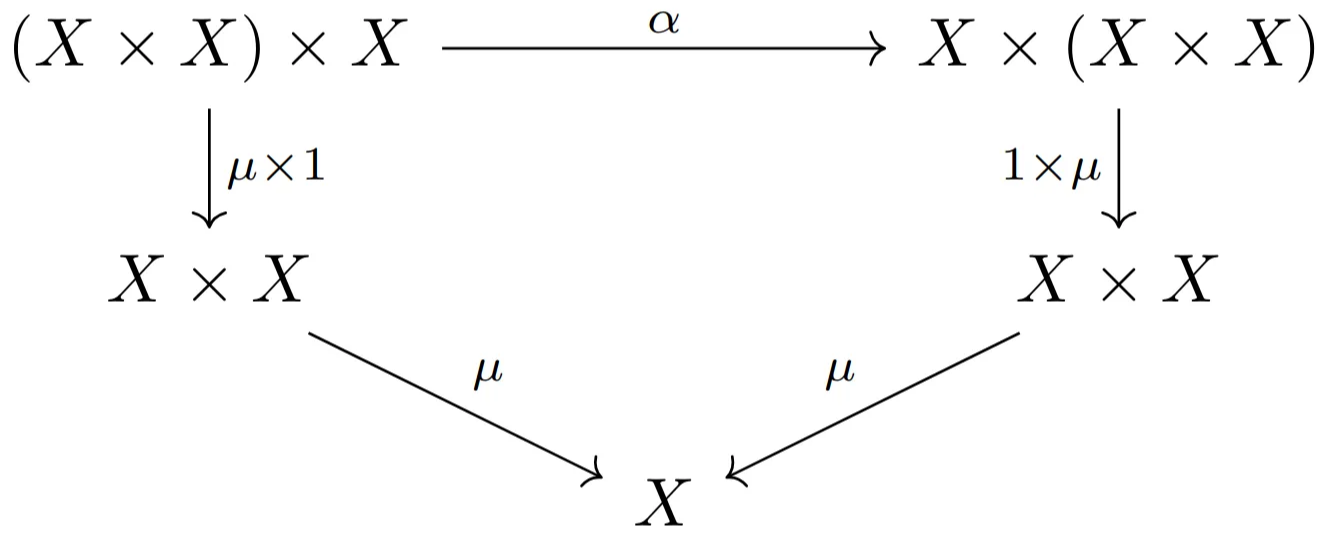
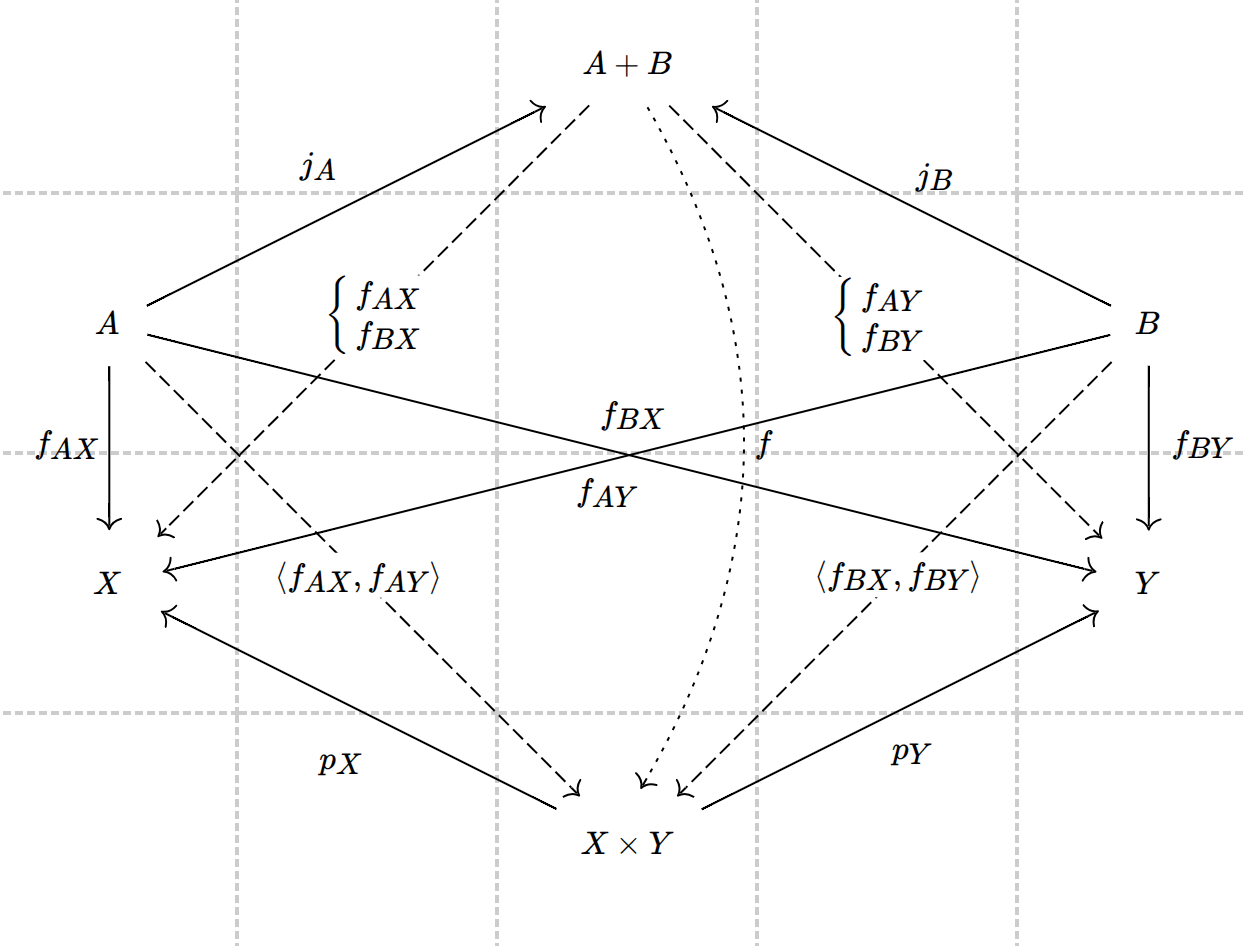
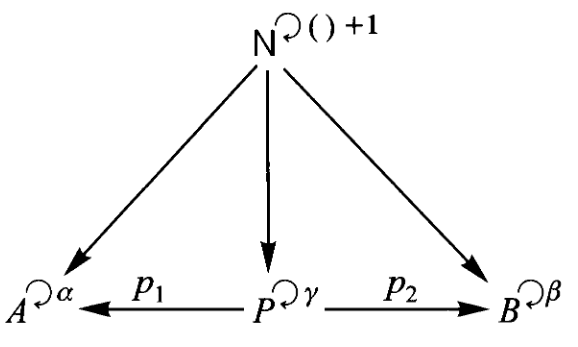
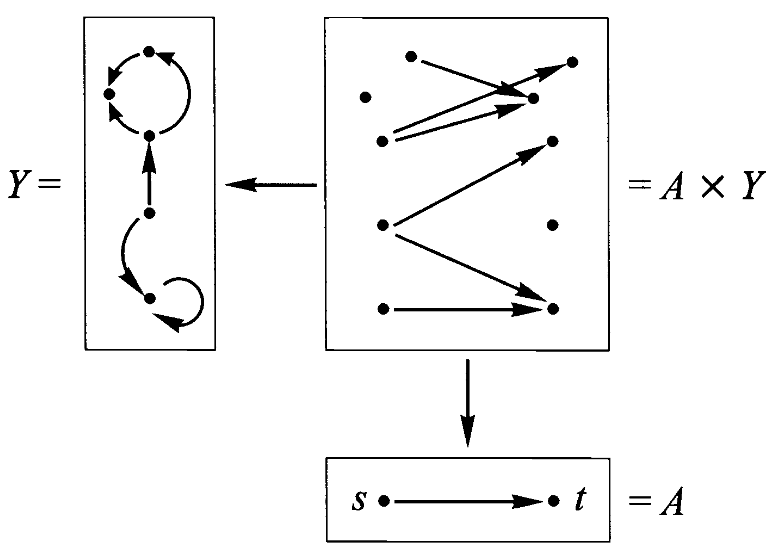
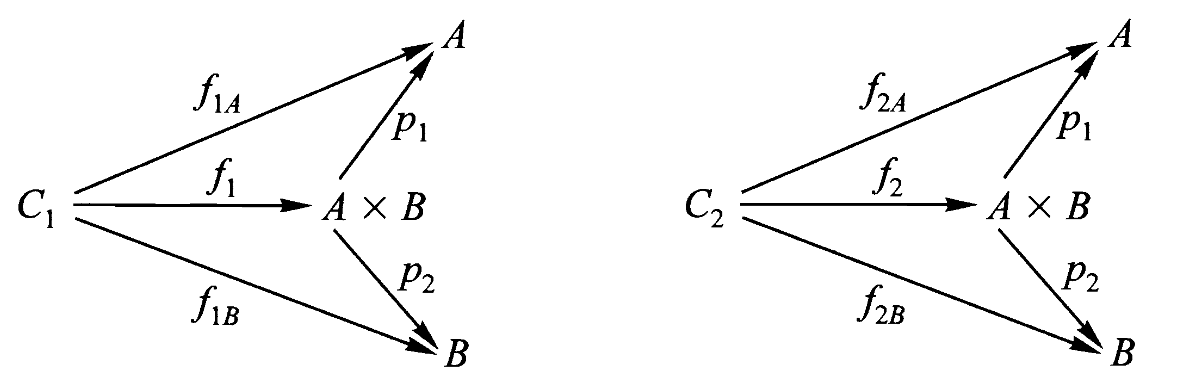
4、积
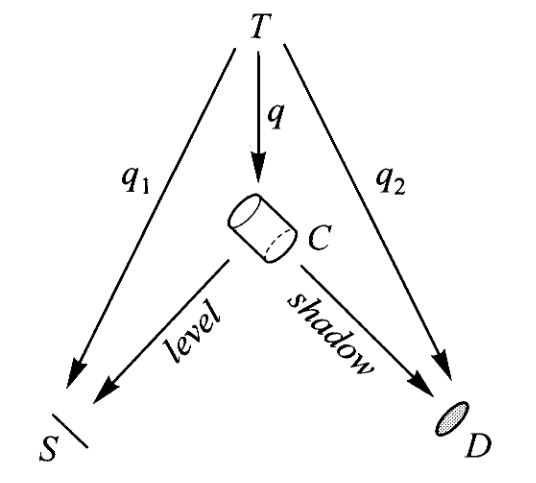
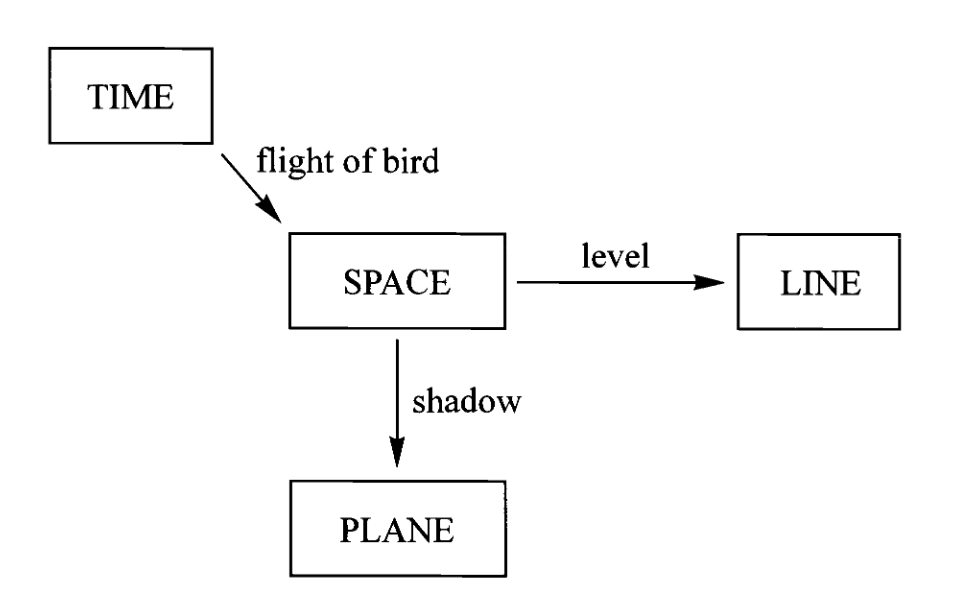
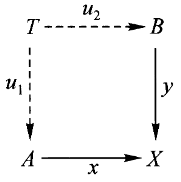
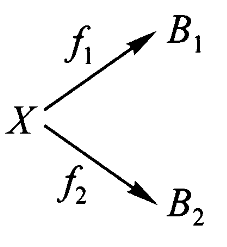
现在我们来讨论一个重要的泛性质,它可以被视为“与”(且、并) and 这个词的客观内容,正如伽利略观察到的那样,空间中的运动等同于水平面上的运动与垂直线上的运动。
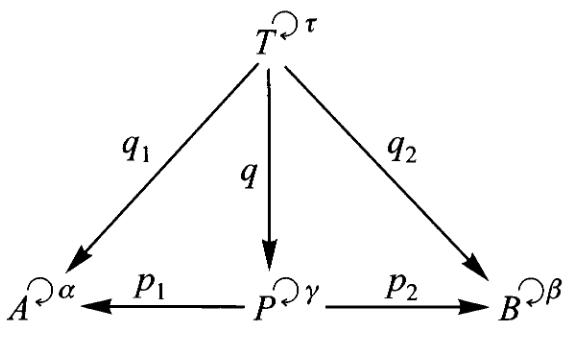
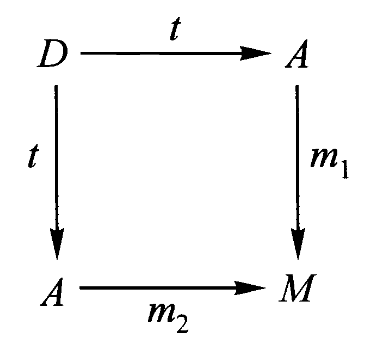
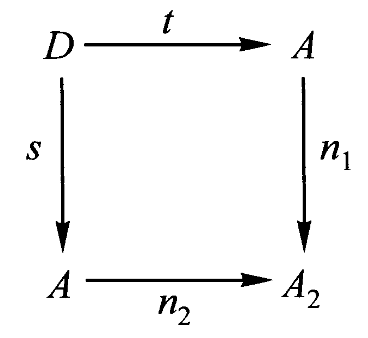
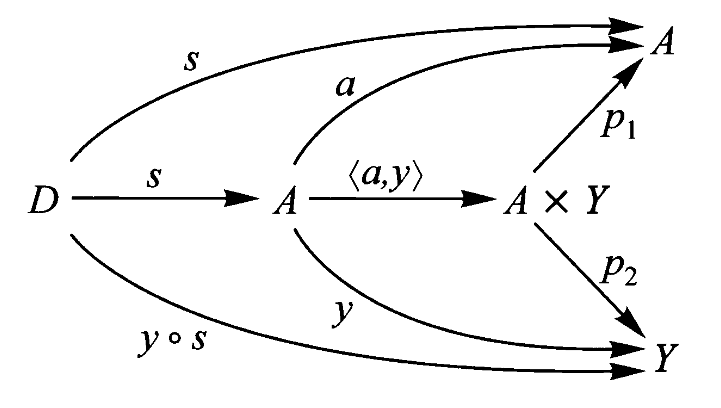
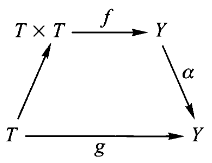
假设
如果有合成则必有分解,这里
就是 的分解。
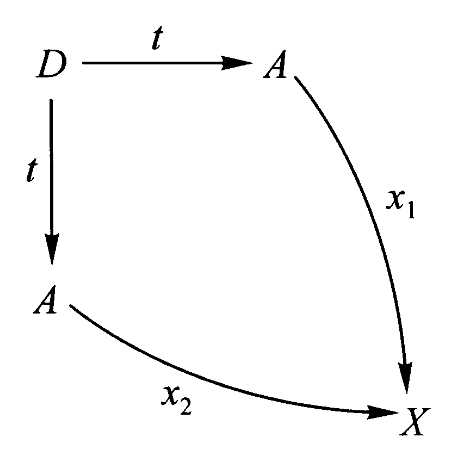
通过仔细筛选
定义:一个对象
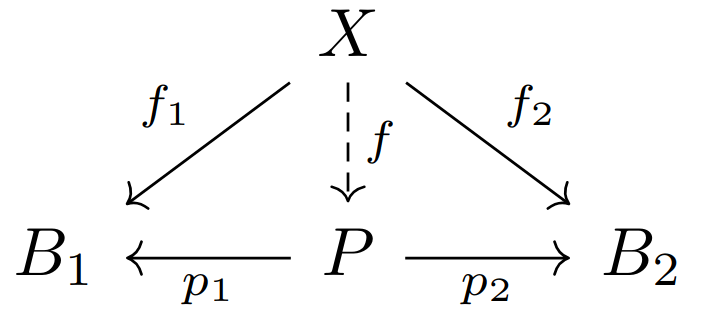
该映射
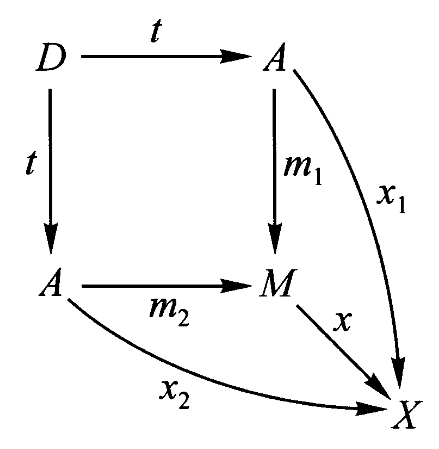
如果有分解,则可以通过积对象来找到合成。这里透过分解
找到了合成 。
练习12:在任意范畴中,若
证明:
首先由
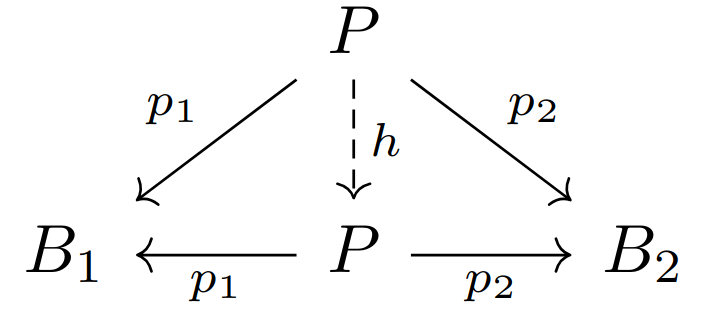
由
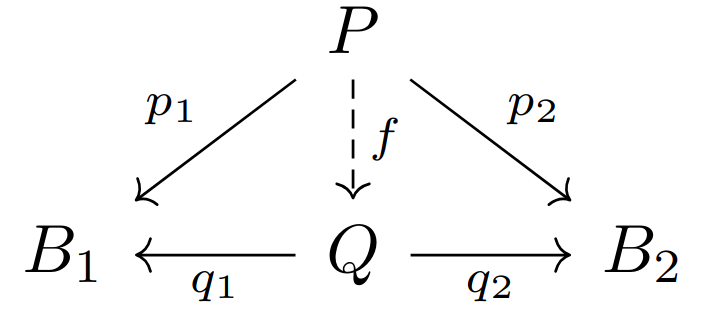
对称的由
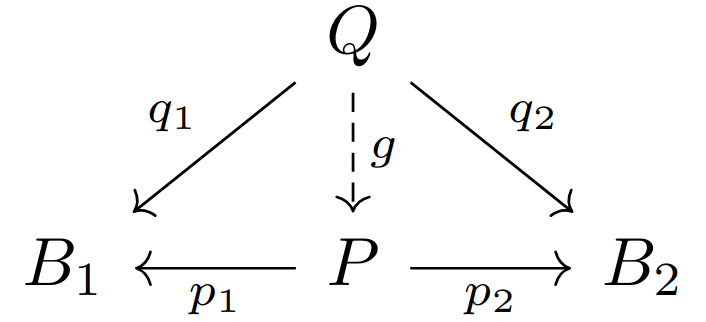
把这两幅交换图拼接在一起,就有
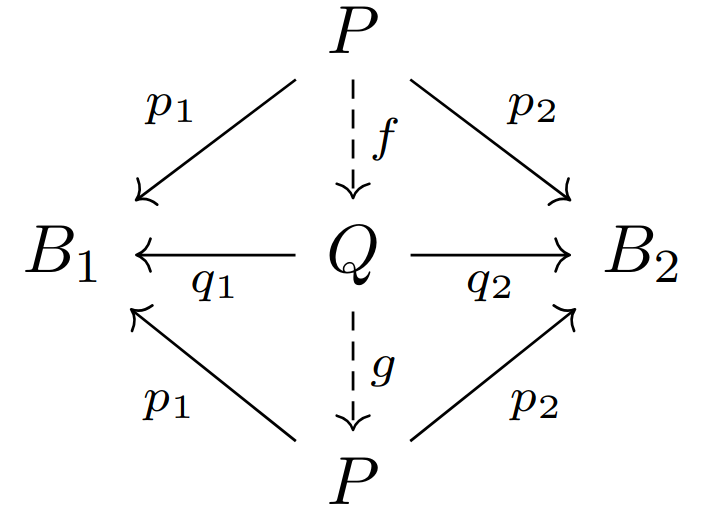
交换。特别的路径
该练习说明对
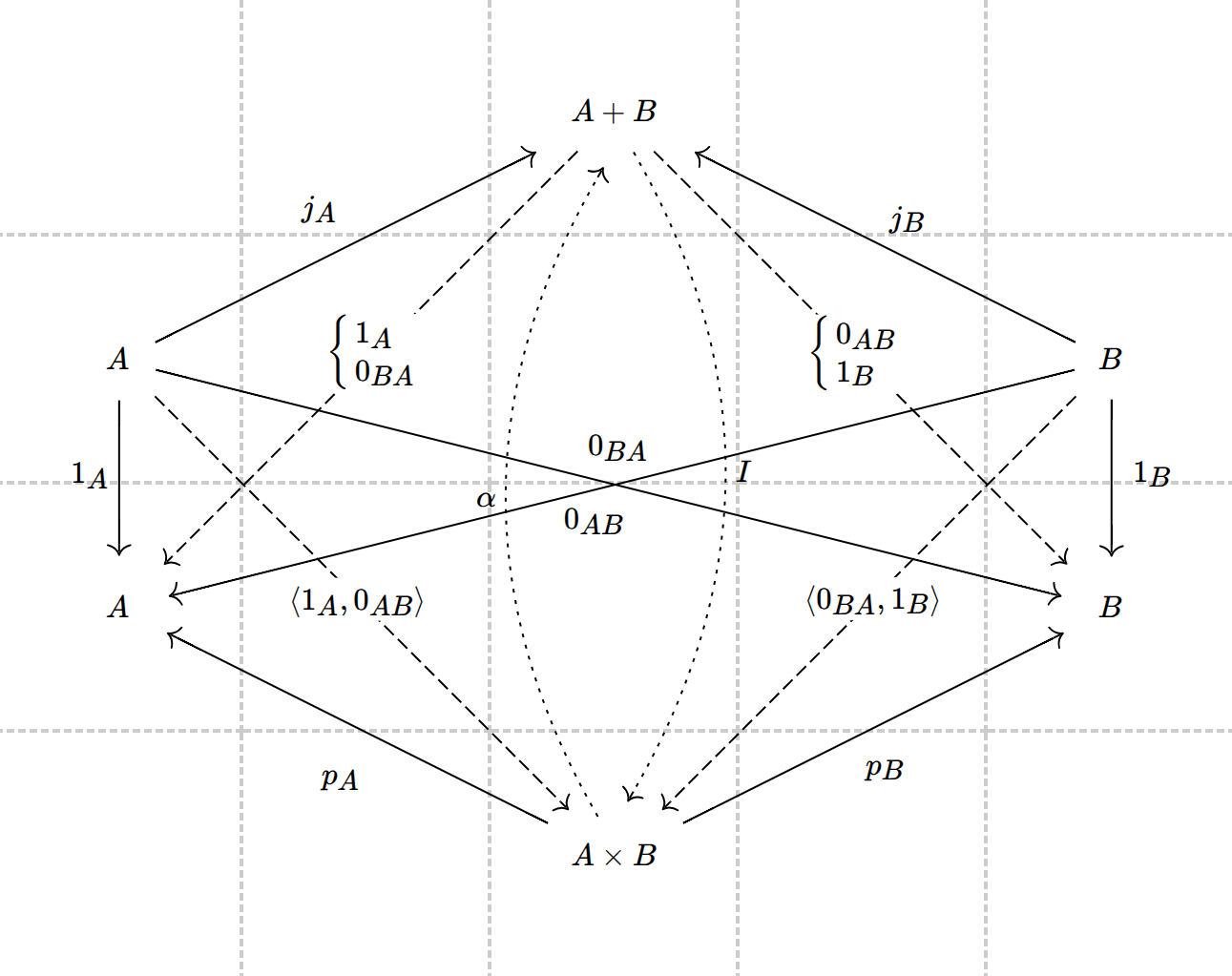
练习13:在任意范畴中,若存在积对象和终对象,那么积对象
证明:考虑下面的交换图,其中
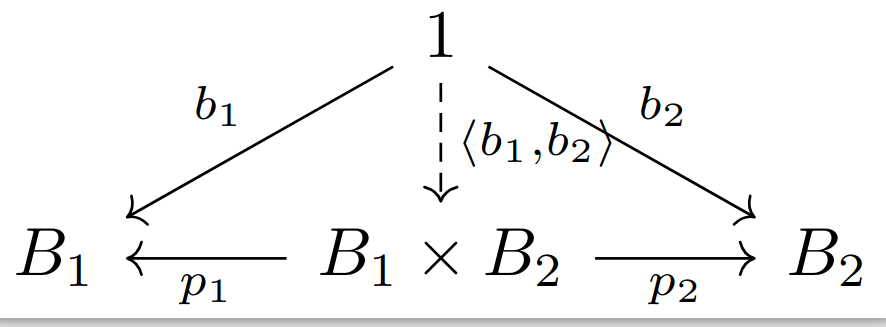
后半句:由
前半句:对
若
其中,线上方的单个映射和线下方的成对映射之间的对应关系通过与投射的复合实现。
回忆点映射(即定义域为终对象的映射)给出了我们重要信息,这说明终对象并非是平凡的。类似的,以积对象为定义域的映射
定义:对象上的一个二元运算 binary operation
例如视自然数集
而作用
注意此时乘法记号的含义,范畴间的乘积运算和数的乘法运算在形式上相仿了。我们具体证明二者是同构的,考虑以下交换图
其中映射
的存在是终对象的泛性质保证的,由此只存在唯一的映射 使得该图交换,记其为 。那么由此可知 。反过来,下面交换图成立
特别的,考虑映射
,由于它是 的映射,那么根据积的泛性质中的唯一性,它只能等于 。因此 与 同构。类似的可以证明 与 同构。
其实,我们例子中的自态射范畴可以推广到任意范畴
该作用结构的保持方程还可以用另一种方式表达,如果我们定义
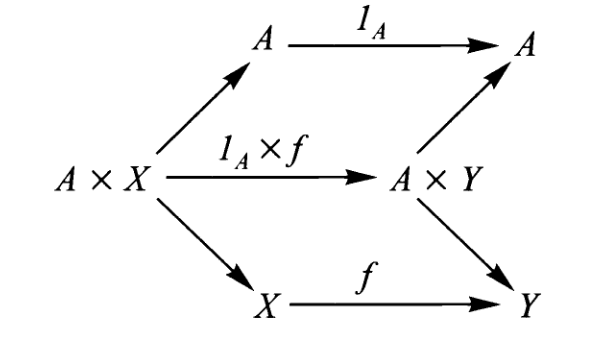
由于
根据这个定义,我们可以把上面的结构保持方程重写为
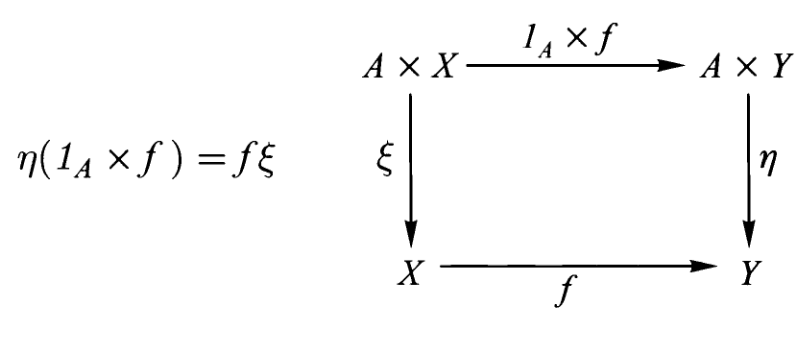
注意在定义
中, 投射 与作用 并不一定相同。 其实可以看成如何把因子上的态射延拓到积上的一种方法,其办法是保持无关因子上的元素(恒等映射 )而只改变相关因子上的元素,最后把二者结合起来。 我们同时可以注意到,按照这个定义
,也就是说形式上可以按分量计算该映射的值。
练习14:定义范畴
解答:
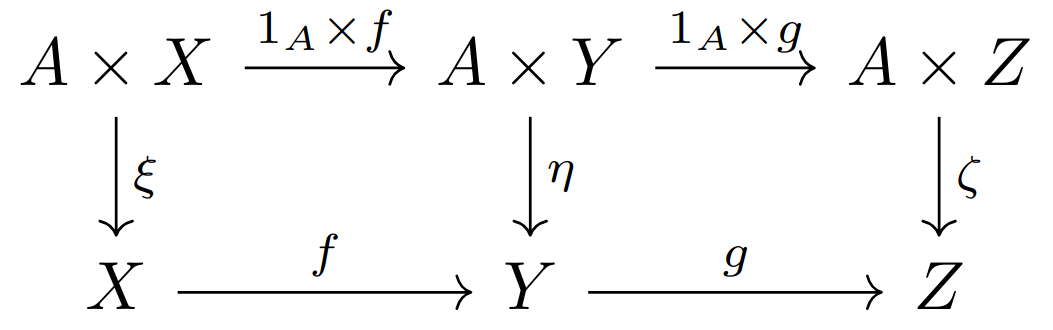
我们可以很自然的定义从作用
此外为证明它确实构成范畴,还需要证明恒等映射的存在,显然
若
练习15:把上述方程用交换图的形式,结合
该练习原书排版有问题。
解答:首先我们尚未定义两个连乘积,特别是我们还没有定义两个连乘积没有括号情况的计算顺序。我们先证明在
定义:给定对象
显然这个定义可以推广到任意有限个因子积。
下面证明三因子积
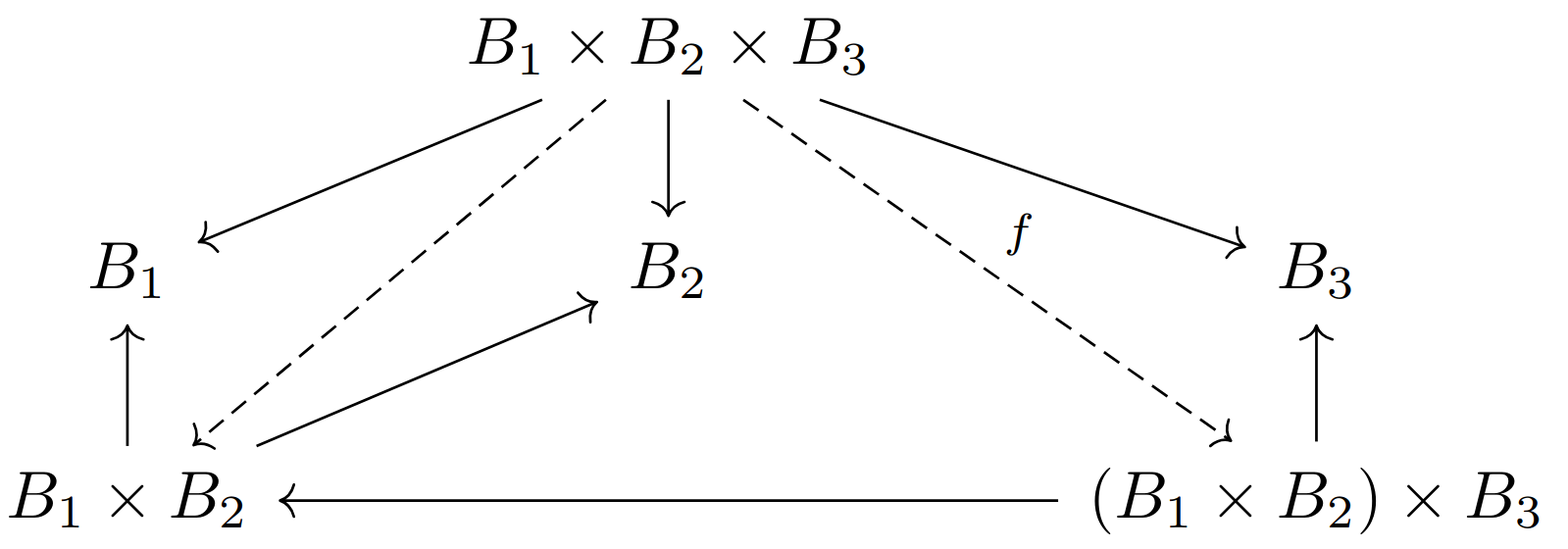
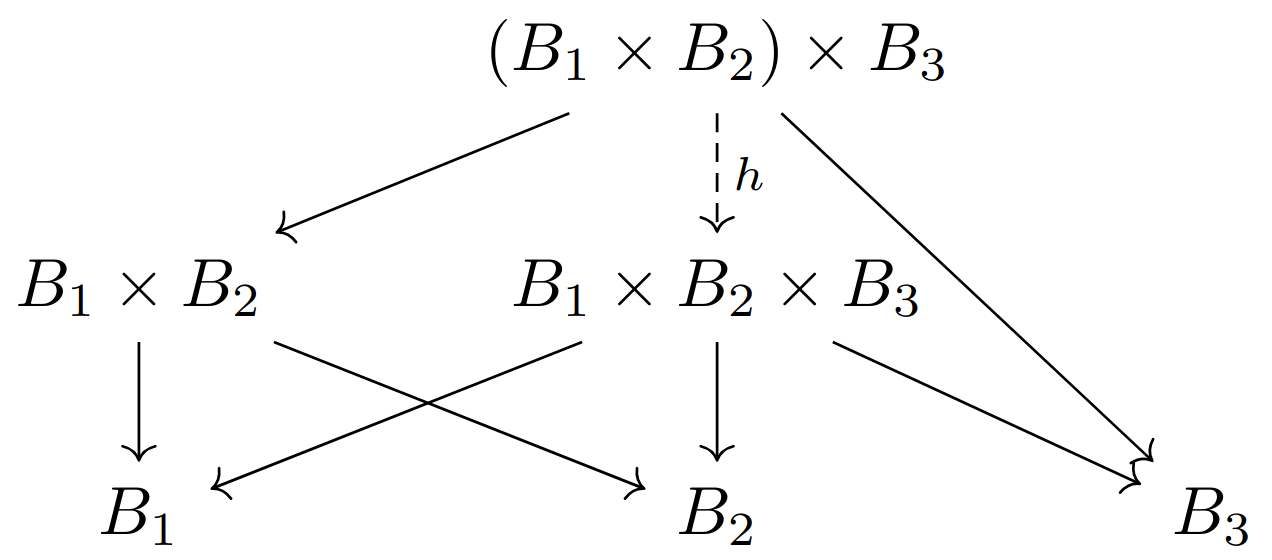
其中实线箭头为积对象配备的投射,虚线箭头为根据积的泛性质诱导出来的存在唯一映射。注意将上下两个图拼接起来,我们就得到存在唯一的映射
下面我们可以正式开始解答该练习。
考虑下面两个交换图所定义的映射
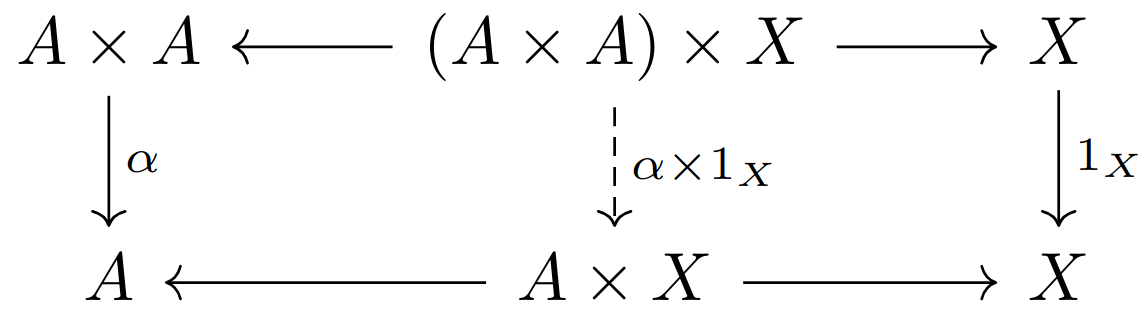
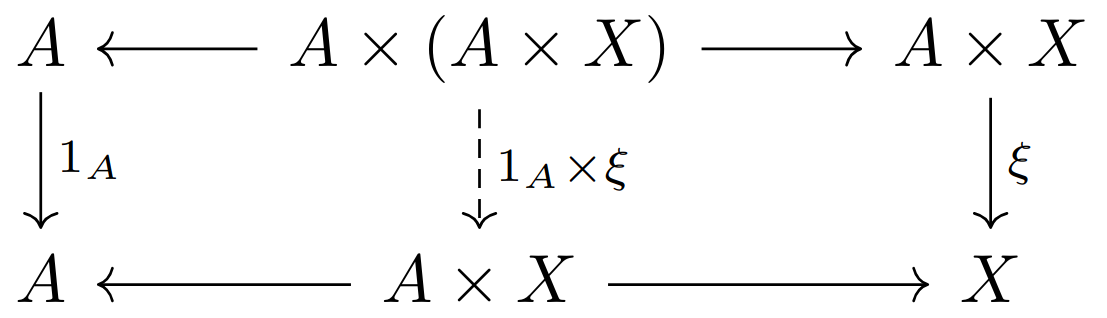
那么第一个方程可以表示为下面的交换图成立
第二个方程则可以表示为下面的交换图成立
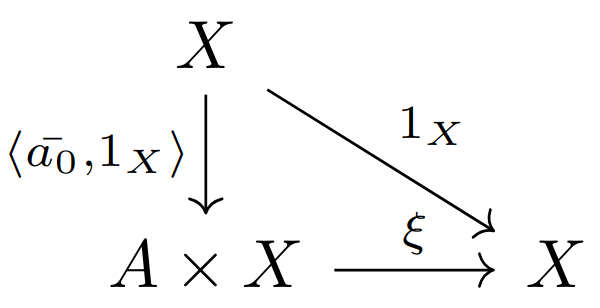
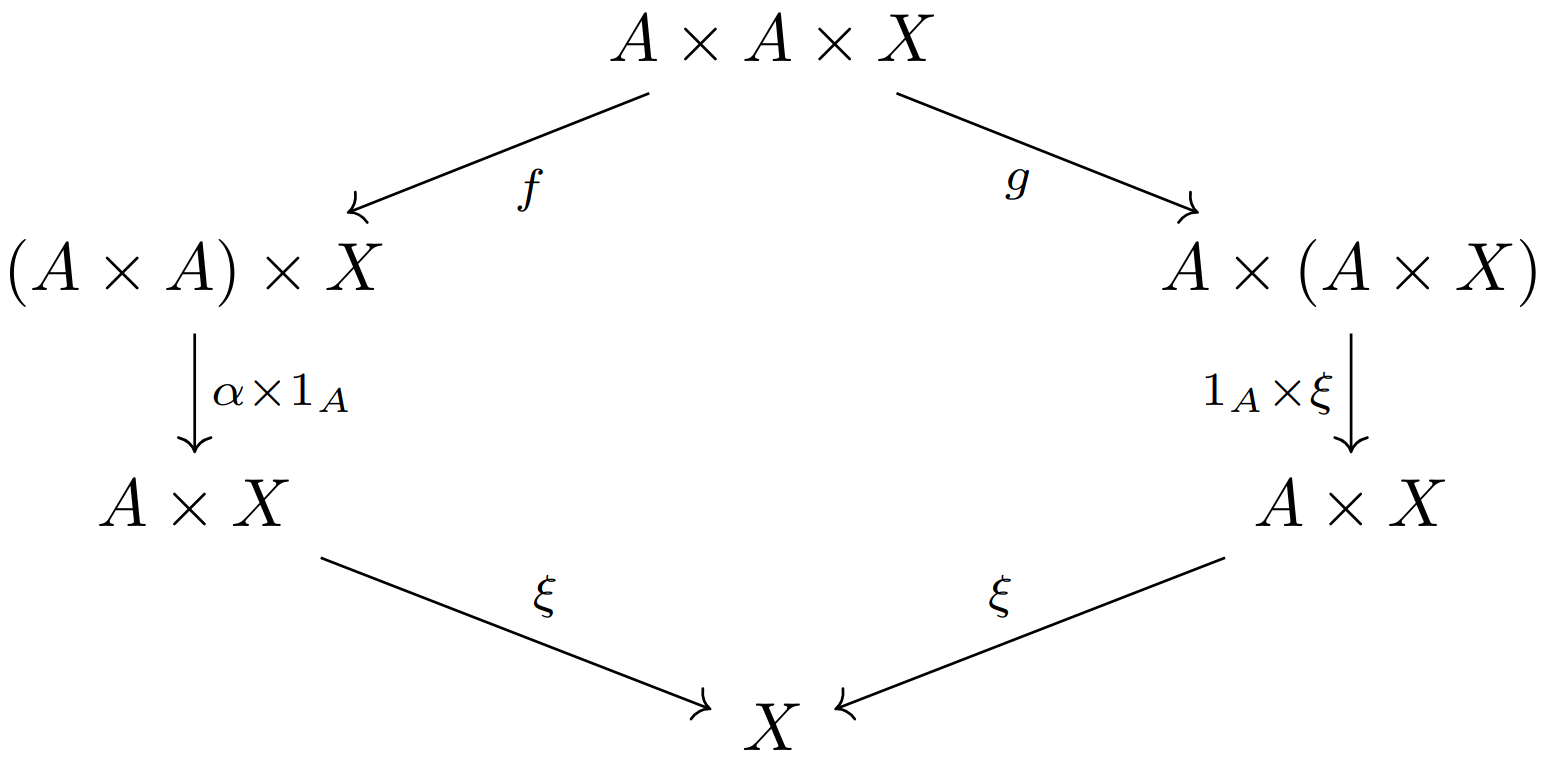
其中
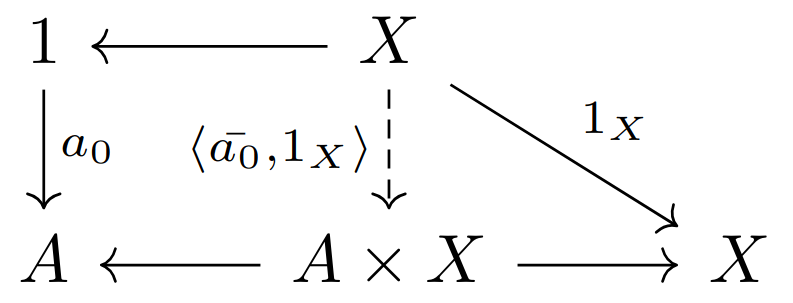
当
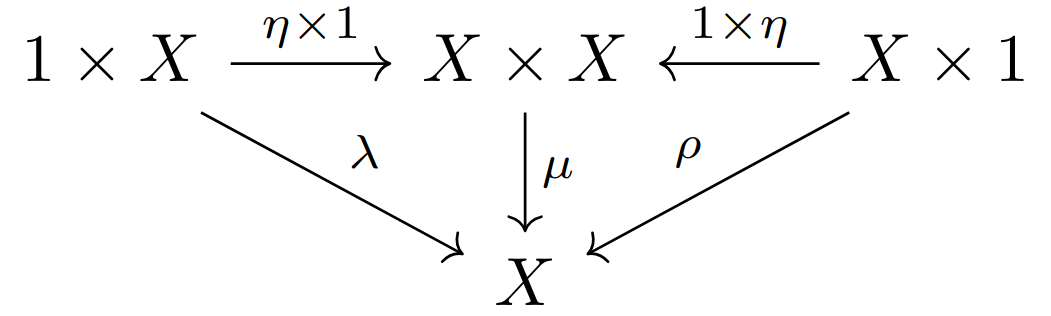
这句话怎么理解?首先,为什么这三者构成一个单元范畴?在会话十三中,单元范畴的定义仅仅是一个仅含单个对象的范畴。查阅范畴论的其他文献知道,这并非单元范畴(或称幺半群)的标准定义。(事实上,本书还混淆了幺半群 monoid 和幺半范畴 monoidal category 的区别,本书中把幺半群 monoid 说成是只含一个对象的范畴,然而幺半群其实应该定义为幺半范畴中的一个对象,而幺半范畴也未必仅含一个对象。) 幺半群的标准定义涉及到幺半范畴的定义(见维基百科),但这里我们简化如下:幺半群是一个对象
,配备乘积映射 与单位映射 ,并使下图交换:
其中
是上面我们刚刚证明的同构映射,而 则是我们在 处证明的同构。写成方程 。我们可以把 视为结合律,而 视为左乘单位元和右乘单位元操作。 显然,如果
作用满足上述方程,那么当 时,就有 ,即 在标准意义下构成一个幺半群,所谓的相容性就是在这个意义上说的,幺半群的性质可以被视为满足该性质的作用的一个特例。
5、对象乘积的交换律、结合律、恒等律
关于数的乘积,我们知道其交换律、结合律、恒等律
总之,在一系列因子的组成的乘积中,分组并不影响结果,顺序并不影响结果,平凡因子(1)可以省略。因此积完全由非平凡因子决定,只要我们考虑其重数 repetitions。
对于对象的乘法,在任何具有对象乘积和终端对象的范畴
首先我们需要关于族 family 的记号,令
定义:一个以
定理(积的唯一性):若映射族
证明:仿照两对象乘积即可。
交换律、结合律和恒等律均可由这个唯一性定理得出。其中交换律是显然的,因为在定义中根本没有涉及对象的顺序,而结合律则可以通过把指标集分成若干个子指标集的并即可,至于恒等律参照我们上面关于
练习16:证明若
则,
是三元积,即满足三元积的泛性质。
证明:略,我们上一节已经证明了这一点。
该练习除了证明迭代乘积
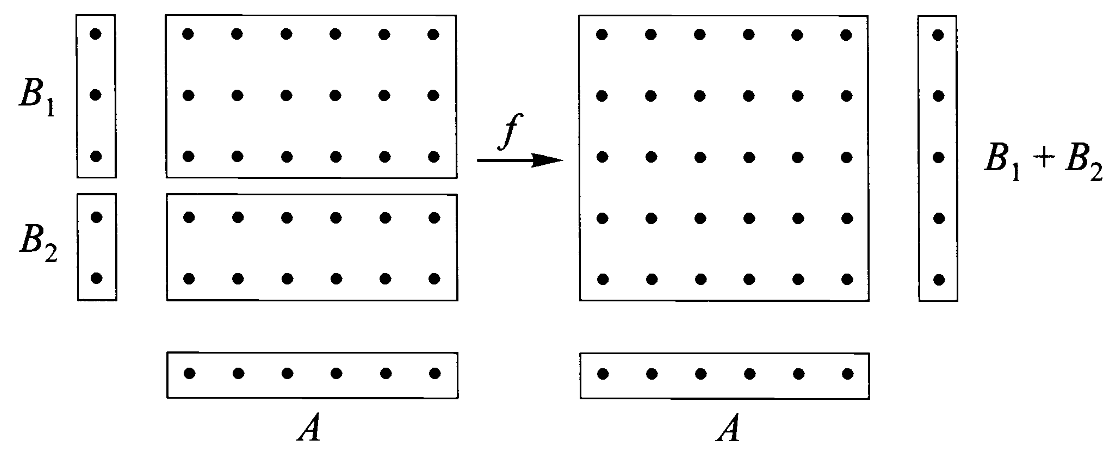
6、和
如果我们对偶化积-投射的概念,就会得到:
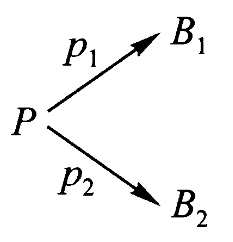
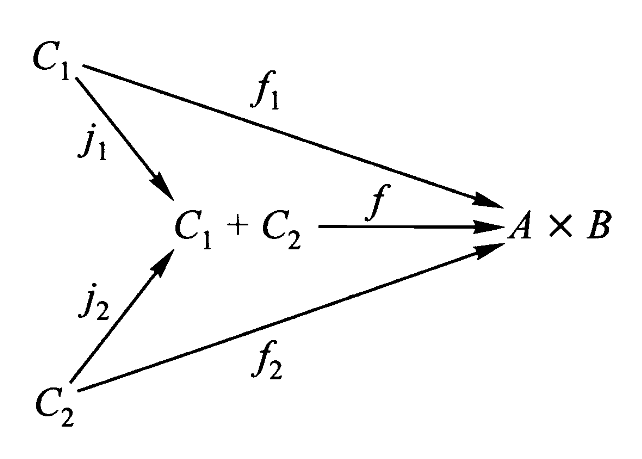
定义:一对范畴映射
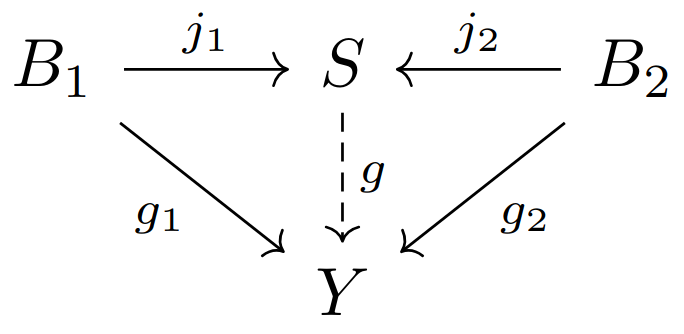
注记:称
练习17:在集合范畴、自态射范畴和图范畴中,和具有以下性质,
证明:首先看出该命题的逆命题对任意范畴成立,即对
在集合范畴中,
对自态射范畴而言,我们知道对象的一点是自态射的不动点,这就意味着和对象中的一点要么是
对图范畴而言,我们知道对象的一点是图中的环,这就意味着和对象中的一点要么是图
练习18:在集合范畴中,存在许多映射
解答:题目实际上要我们找到这样的例子:
练习19:证明
证明:略。
更一般的和也遵循交换律、结合律、恒等律(其中恒等律涉及的是始对象
)。也可以定义更一般的指标集标记的对象族的和。而由于和与积的对偶性以及始对象与终对象的对偶性,这些证明可以统统在箭头反转之后得到完全相似的证明。
7、分配律
尽管我们看到在任何范畴中,对象积与和遵循与数的运算中的相似定律。但是把加法与乘法关联起来的分配律
其实,至少有一个映射将等式两侧的对象关联起来。对任意同时含有和、积、始对象的范畴而言,可以只用关系中的注射和投射与映射的泛性质来确定标准映射:
证明:第二个式子由始对象的泛性质是显然的(而且唯一)。第一个标准映射的存在则考虑下图
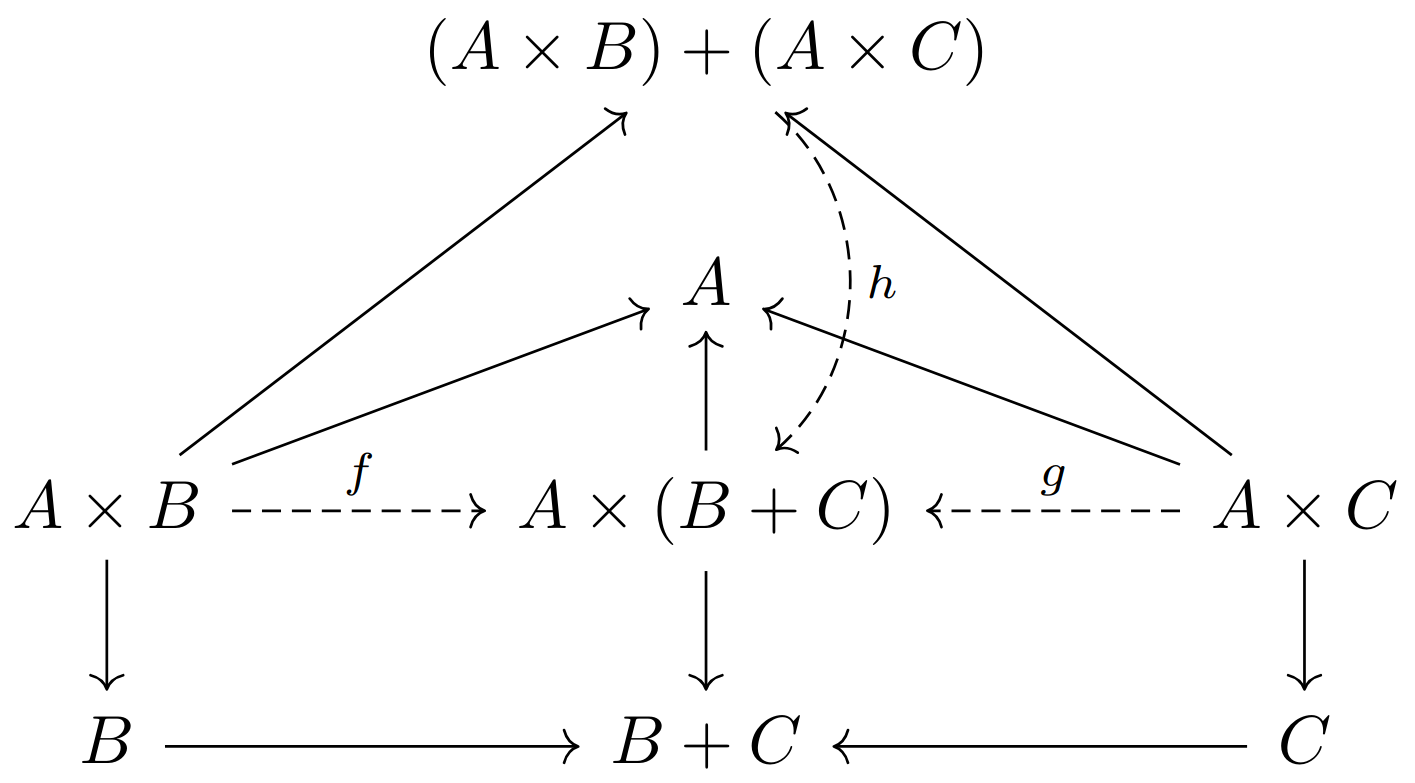
其中对
但是我们并不能保证这个映射是同构。
定义:一个范畴称为满足分配律,如果上述映射在该范畴中是同构映射。
例如在集合范畴,自态射范畴和图范畴中,分配律都成立。我们将在第五部分中使用指数映射来证明这一点。
练习20:带点集范畴
考虑带点集的和,它需要满足基点的注射也到基点,也就是说若
当然如果
则分配律成立,这是唯一使分配律成立的可能。因为此时有乘法恒等律的帮忙。
练习21:记
证明:记
这里具体如何计算图映射的积和和对象?首先把它们都视为集合范畴中的对象(即忽略箭头),因而积对象和和对象分别是集合的笛卡尔积和无交并;然后根据投射或嵌入映射的对应性,在这些集合中添加箭头。具体的细节详见下文的会话。
8、导览
泛性质被认为是对象乘法和加法的来源;在第十九讲到第二十八讲中将更深入更广泛的讨论这些构造,如何使用、计算它们。加法和乘法之间的关系,如分配律,是更深层次的内容;这些内容的讨论将从第 25 讲末尾开始。第 28 讲之后是一些抽测。在第 29 讲中,我们将学习积的另一个性质,它将在第五部分中被提升到更高的层次。
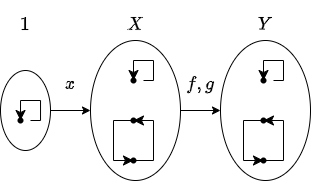
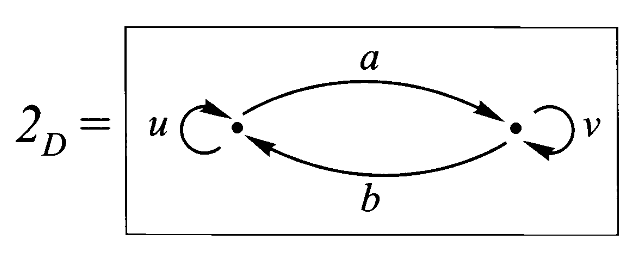
第十九讲、终对象
现在我们来讨论乘法的单位元,“一”。你已经见过几种不同的 "一"。其一是数字 1,数乘法的单位满足:对于每个数
对任何集合
第四篇中的终对象定义里的
自态射范畴中的终对象是什么呢?猜想到是单元集配上恒等映射。为了证明这一点,考虑任意动力系统映射
对图映射而言,情况又如何?如果记
且映射
注意可能有人猜想终图只是一个孤立点,但对任何有箭头的图而言,都不存在从它到孤立点图的映射
第二十讲、对象的点
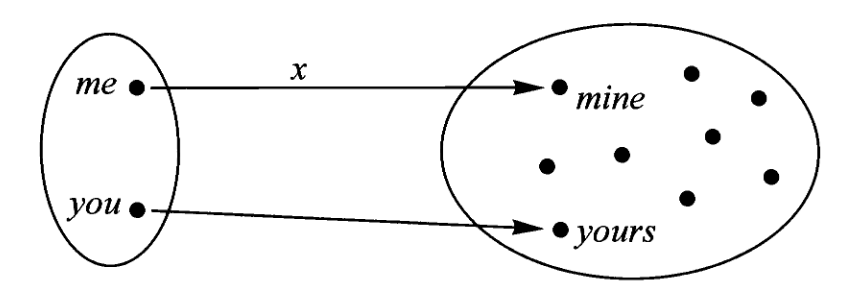
此前我们已经强调过任何集合的性质都可以表达为集合范畴中映射与映射的复合。例如集合中的元素或一点可以定义为从终对象(单元集)
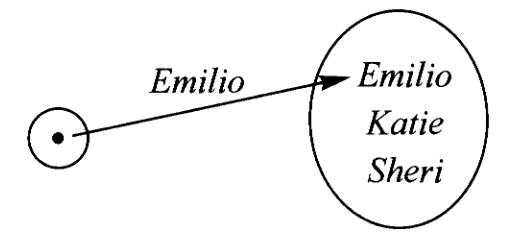
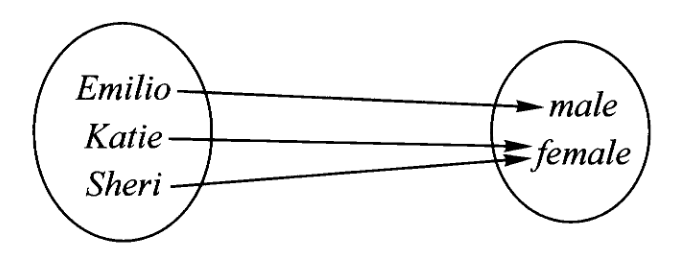
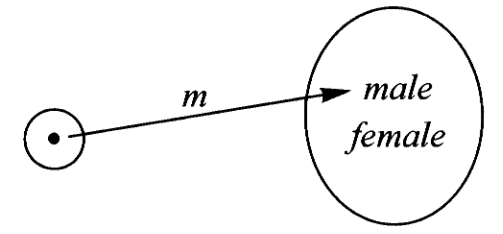
特别的,如果我们为了判断某人的性别就可以通过映射的复合来表达,例如
既然任意集合中的每个元素都有个从终对象出发的映射对应,而终对象本身也是一个单元集,那么它背后的对象与映射是什么呢?还是终对象,而那个映射就是终对象上的同构映射。
由于我们在集合范畴中定义了点映射为从单元集出发的映射,而为了将这一概念推广到任意范畴,我们把单元集的泛性质提取出来,仅依靠映射关系来描述它,即点映射是从终对象出发的映射。
但是在其他范畴中,点映射就无法表示所有元素了(这里谈元素特指那些基于集合搭建的范畴),例如在自态射范畴中,终对象为单点自态射,因此从它出发的点映射的像也只能是自态射的不动点。不过在这个范畴中,我们可以找到其他对象能够表达自态射范畴中的任意点,即
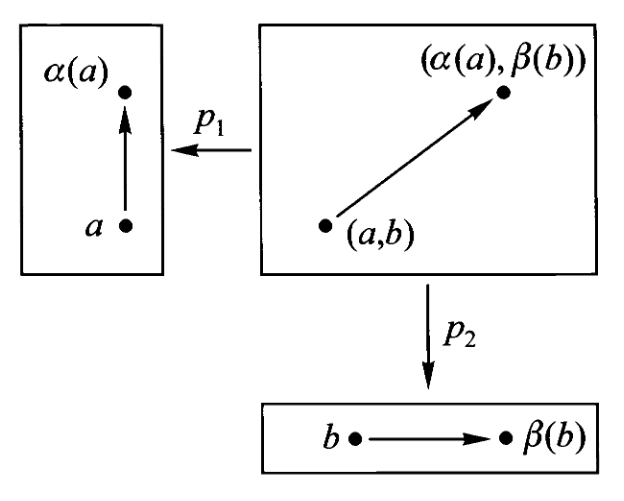
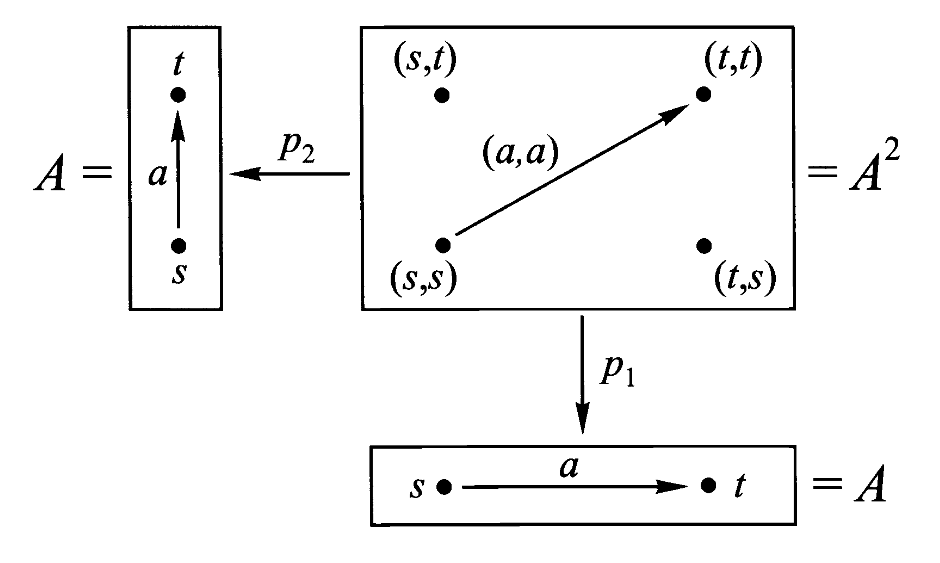
第二十一讲、范畴的积
回忆我们在第一讲中提到的伽利略关于运动的分解图景,通过范畴的积我们将更清晰的表达这个概念。
通过把圆盘乘上线段,我们得到了圆柱
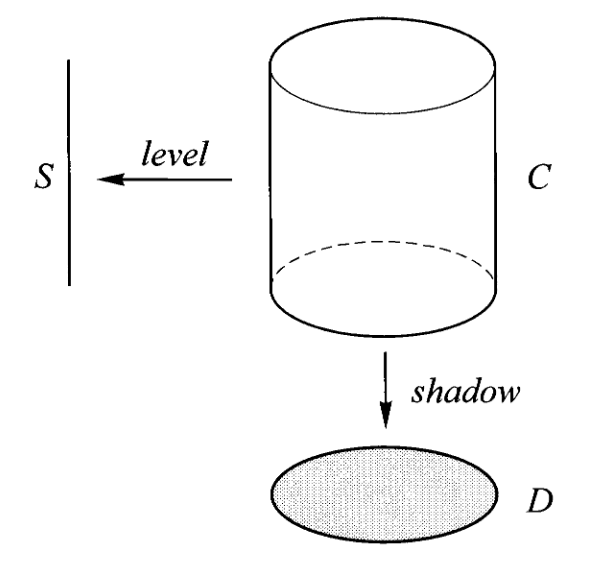
注意这里不是简单的体积等于面积乘高度,而是集合中元素的对应,即圆柱上任意一点都可以表示为线段上一点乘上圆盘上一点。因此当我们把两个对象相乘,我们不仅仅得到了第三个对象,还顺势获得了乘积与因子间的关系,即从乘积到因子的投影映射,它告诉我们乘积如何由因子组成,或者说乘积的元素如何分解为因子的元素。
因此,任何在圆柱上的运动
它完全是我们在第一讲中见过的图式的翻版。进一步的如果我们抛开物理意义,把定义域
注记:类比数的乘法,在对象的乘法中,我们把部分称为因子 factor 而把总体称为积 product。在我们下面提及对象的加法时,我们把部分称为被加数 summand 而总体称为和 sum。
我更倾向于把 summand 翻译为和因子,或者在不混淆的情况下简称为因子。
更严谨的说,对象的积不仅仅指那个积对象,还包含两个投影映射,但为了叙述方便我们当我们说积对象时,必然暗含它配有两个投影映射。
根据积的泛性质,投影映射必然是满射,因为
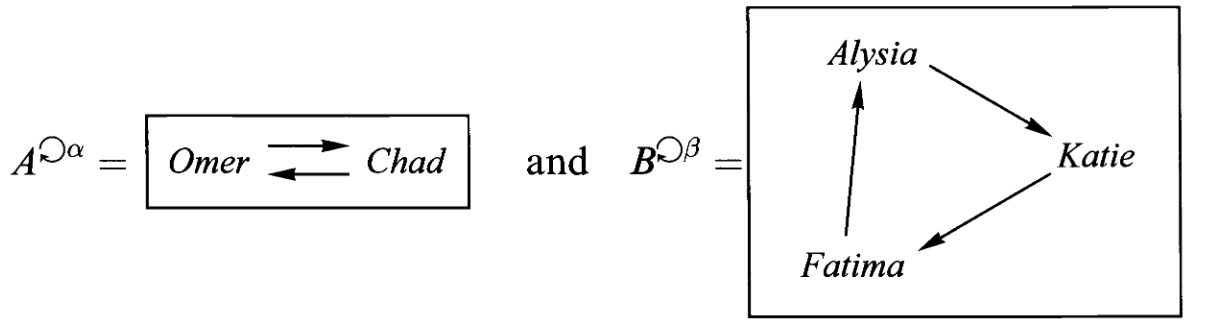
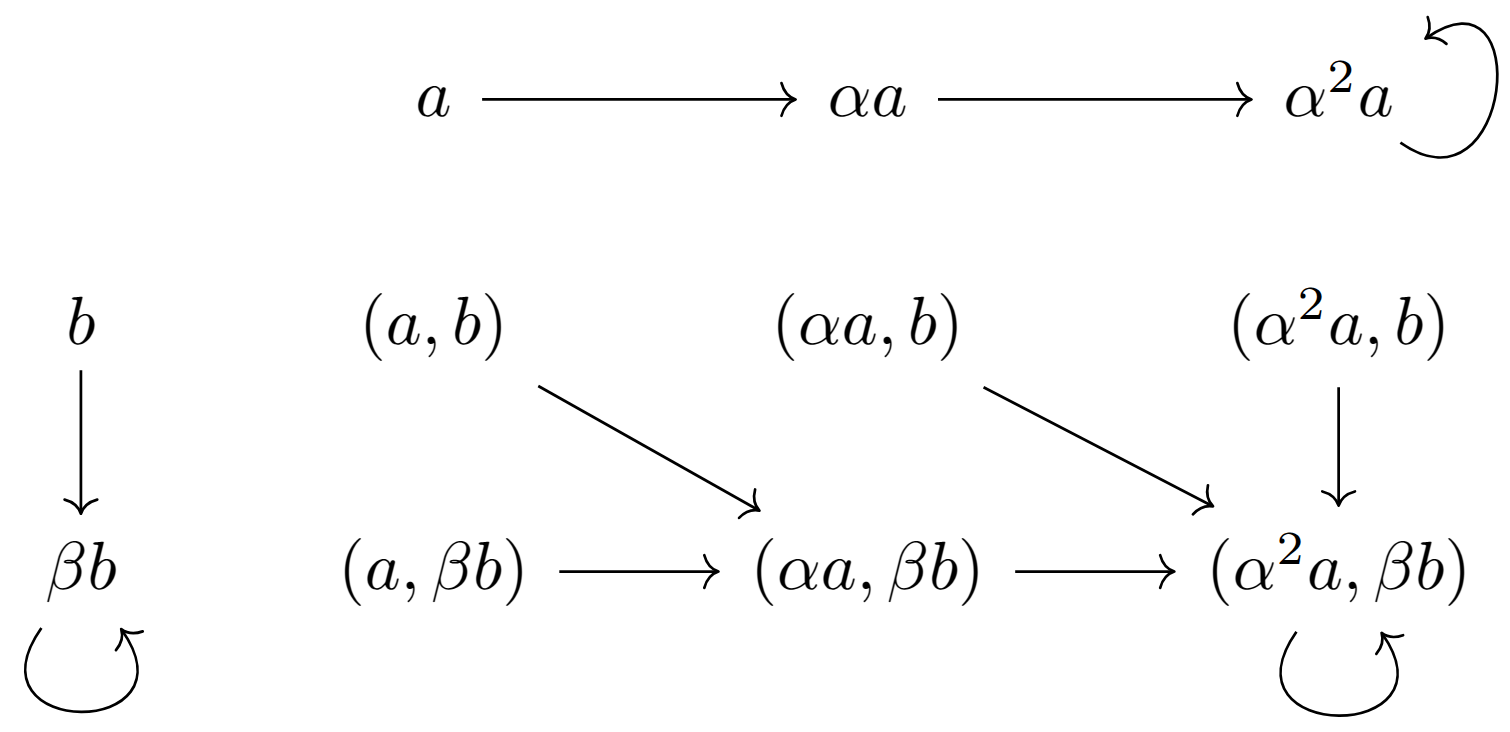
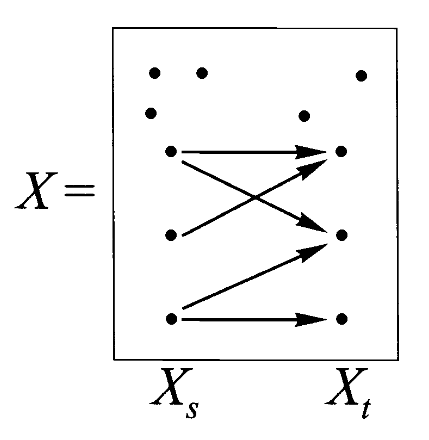
下面我们来探讨自态射范畴中的积。考虑两个自态射集合
显然有映射
在此基础上,是否可以把
再考虑另一个例子,一间工厂的工人实行下面的三班倒制度:
夜班 night shift:0到8点,白班 day shift:8到16点,晚班 evening shift:16点到(次日)0点
然后考虑两个自同态集合,一个是一天当中的所有小时
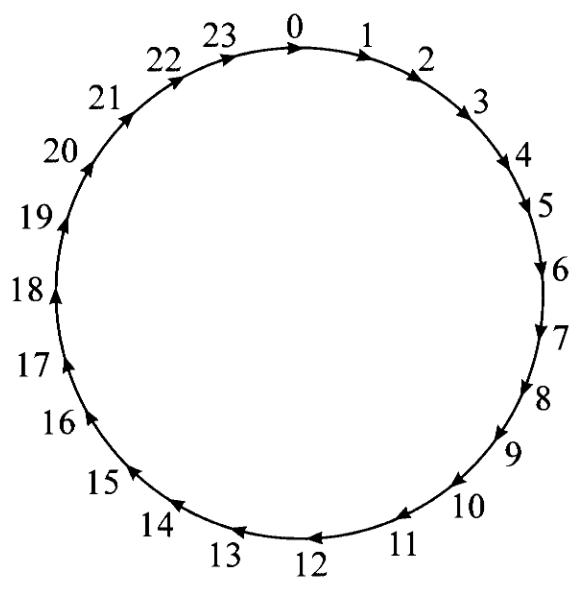
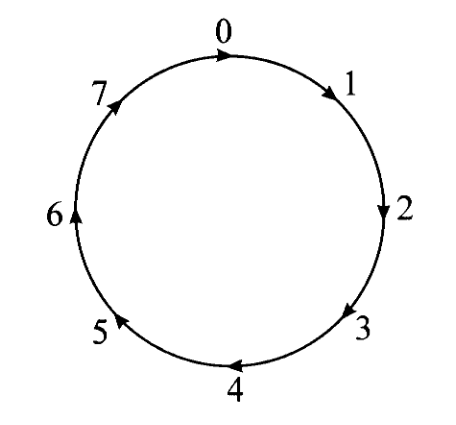
从前者到后者有一个映射,标志着三班倒的工作时间,该映射可以表示为
练习1:是否存在从
假如我们遗忘掉这些集合上的自态射结构,我们容易知道存在在集合范畴上的积关系:
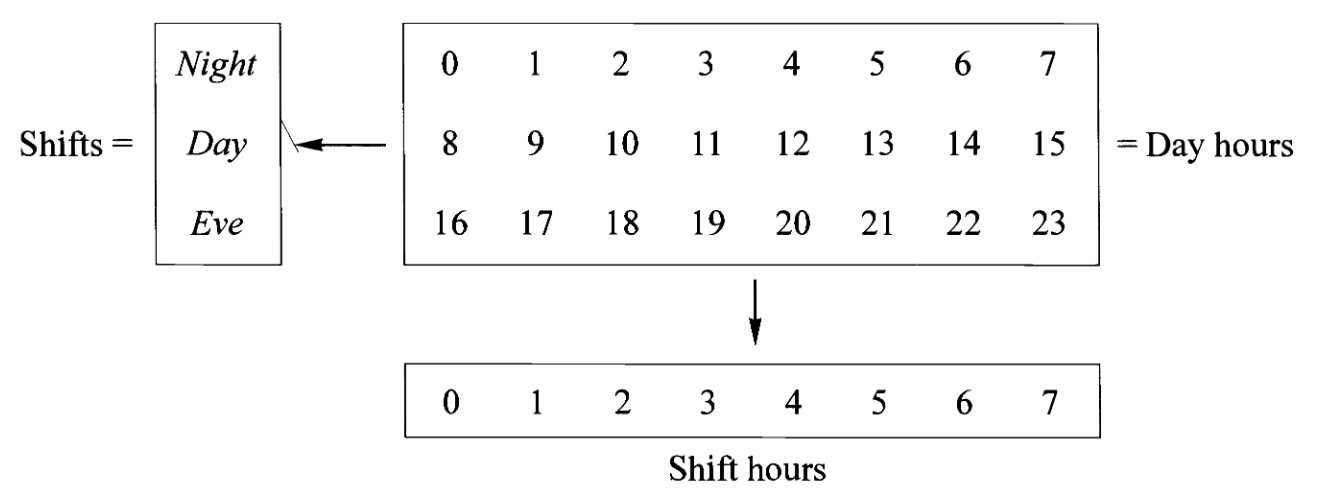
不过集合范畴上的这种积却无法直接作为自态射意义上的积,因为此时表示三班倒的
那么什么样的对象符合这个要求呢?甚至说满足该条件的对象是否存在呢?这其实是一个逆命题,即给定一个对象
为了解决这个问题,我们首先需要研究自态射对象的积有什么性质、长什么样?这样也许能够帮助我们回答
回顾自态射范畴的性质,对任意自态射对象
这就说明
此处的投影映射确实以一种几何意义上的投影表现出来。
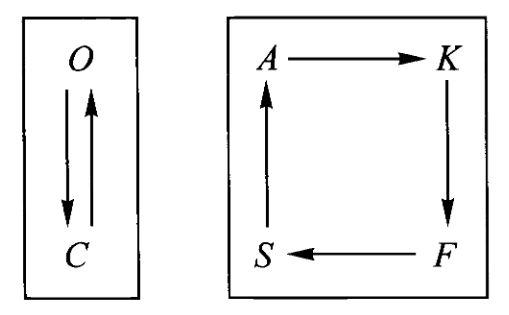
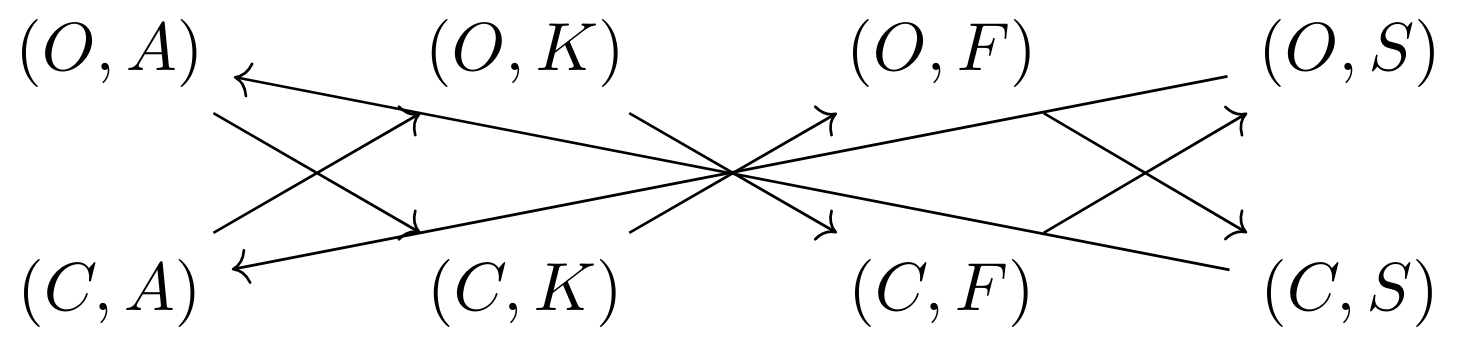
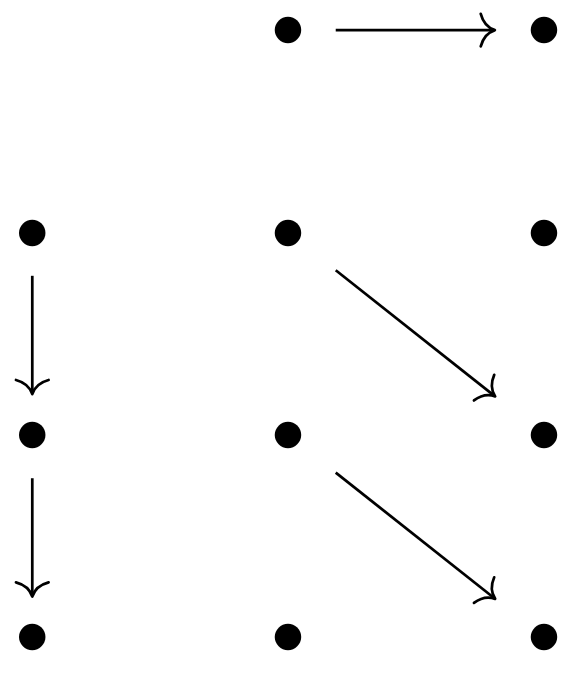
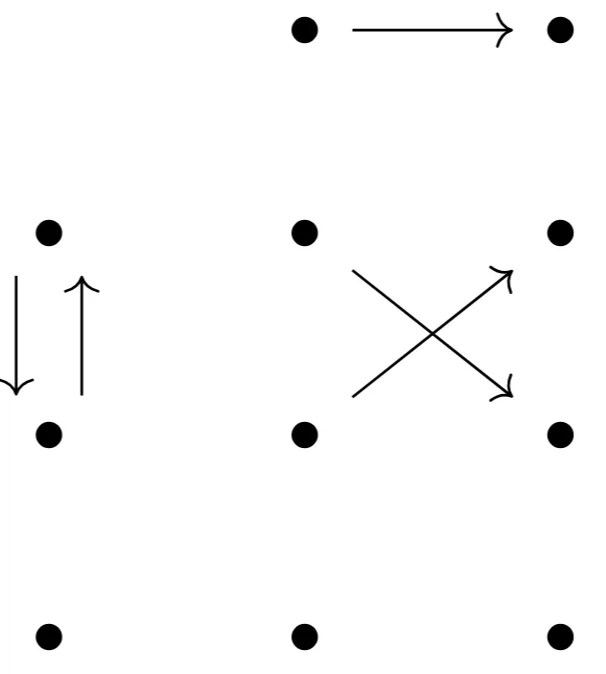
给一个完整的自态射积图式的例子:
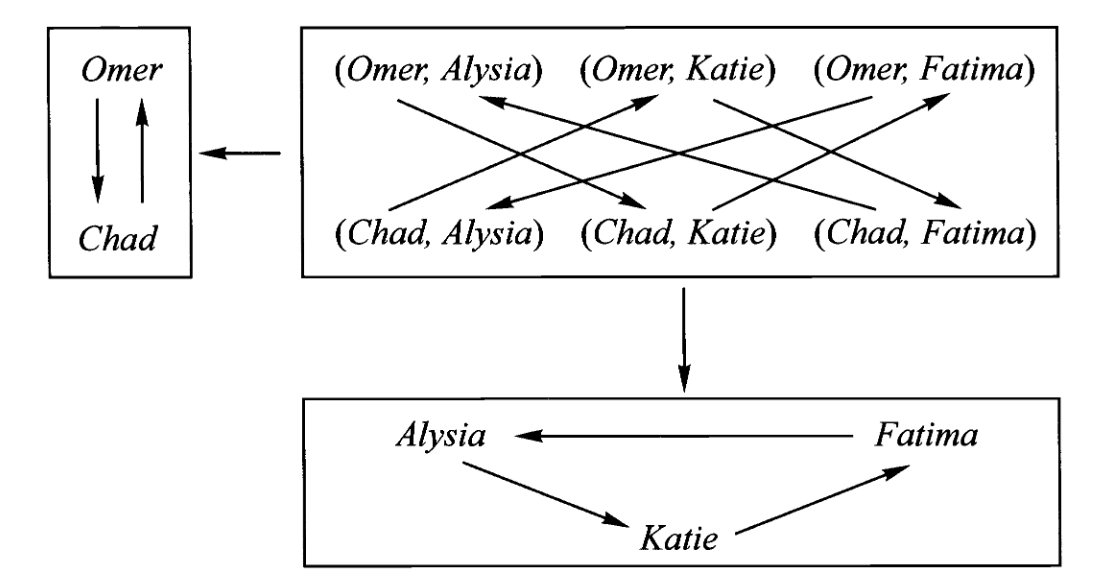
特别的,我们发现一个2-环与一个3-环的乘积是一个6-环。但不要被这简单的关系欺骗了,比如把下面一个2-环和一个4-环乘在一起并不会得到一个8-环,而是两个4-环:
练习2:讨论
解答:首先作为集合,该积对象有
若
证明:不妨设
有解,等价的
根据同余方程组的性质可知,该方程组有解等价于
而我们知道
在给出这个证明以前,我们探讨
m = 8
n = 12
from itertools import product
all = [pair for pair in product(range(m), range(n))]
class Pair:
m = 8
n = 12
def __init__(self, x, y):
self.x = x
self.y = y
def __add__(self, other: "Pair"):
return Pair(self.x + other.x, self.y + other.y)
def to_tuple(self):
return (self.x % Pair.m, self.y % Pair.n)
orbits = []
while all:
orbit = []
repeat = False
p = all.pop(0)
orbit.append(p)
while not repeat:
next_p = (Pair(*p) + Pair(1, 1)).to_tuple()
if next_p not in orbit:
orbit.append(next_p)
print(next_p)
all.remove(next_p)
p = next_p
else:
repeat = True
orbits.append(orbit)
# 可视化部分
import matplotlib.pyplot as plt
import numpy as np
# 示例数据:二维元组列表
colors = ["red", "green", "orange", "blue"]
plt.figure()
# 将点的坐标分别提取为x和y列表
for orbit, color in zip(orbits, colors):
x, y = zip(*orbit)
# 创建一个新的绘图
# 绘制点
plt.scatter(x, y, color="black")
# 计算每个箭头的dx和dy
dx = np.diff(x)
dy = np.diff(y)
# 绘制箭头
plt.quiver(
x[:-1], y[:-1], dx, dy, angles="xy", scale_units="xy", scale=1, color=color
)
plt.xlim(-0.5, 7.5)
plt.ylim(-0.5, 11.5)
plt.xticks(np.arange(0, 8, 1)) # X 轴刻度:0,1,2,...,7
plt.yticks(np.arange(0, 12, 1)) # Y 轴刻度:0,1,2,...,11
# 设置坐标轴比例相同
# plt.axis("equal")
# 显示图形
plt.show()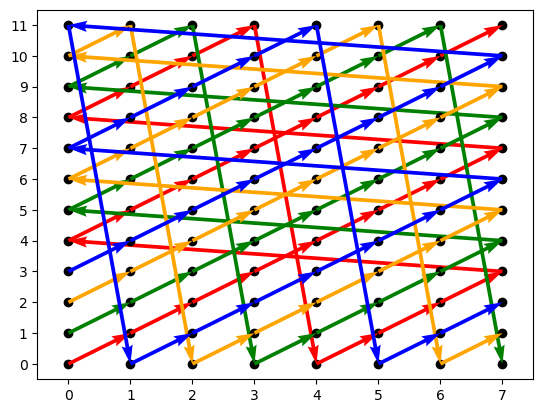
练习3:回到第十二讲的练习3,证明其中称为
解答:
现在我们回过头来审视前面遗留下来的练习1,我们知道
import matplotlib.pyplot as plt
import numpy as np
# 示例数据:二维元组列表
plt.figure()
# 将点的坐标分别提取为x和y列表
# 复用前面的Pair类
Pair.m = 3
Pair.n = 8
orbit = [Pair(i, i).to_tuple() for i in range(24)]
x, y = zip(*orbit)
# 创建一个新的绘图
# 绘制点
plt.scatter(x, y, color="black")
for i, (xi, yi) in enumerate(orbit):
plt.text(xi, yi, f"{i}", fontsize=10, ha="right", va="bottom")
# 计算每个箭头的dx和dy
dx = np.diff(x)
dy = np.diff(y)
# 绘制箭头
plt.quiver(x[:-1], y[:-1], dx, dy, angles="xy", scale_units="xy", scale=1, color='orange')
plt.xlim(-0.5, 2.5)
plt.ylim(-0.5, 7.5)
plt.xticks(np.arange(0, 3, 1)) # X 轴刻度:0,1,2,...,7
plt.yticks(np.arange(0, 8, 1)) # Y 轴刻度:0,1,2,...,11
# 设置坐标轴比例相同
# plt.axis("equal")
# 显示图形
plt.show()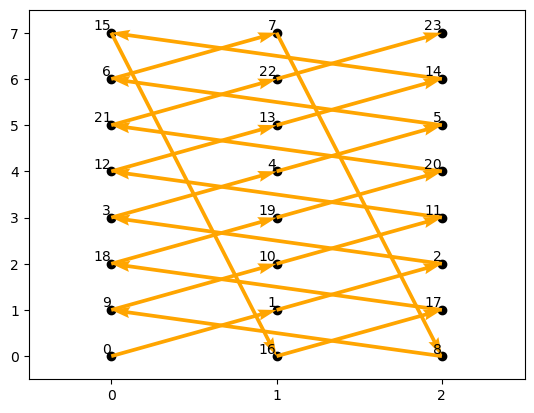
而这里的
第二十二讲、泛性质:相交关系 incidence relations
1、集合范畴的一个特殊性质
我们希望探讨两个相关概念:
- 泛性质
- 用图象 figure 和交互关系 incidence relations 来探测对象的结构
所谓 incidence 指图 graph 中点与线之间的关系,即点是否在某个线上或线是否经过某点。下面我们将讨论图范畴中的相交关系,然而在范畴论的意义下这种相交关系实际上是一种特殊的交换图,因此我们可以推广为交换图中对象与映射的关系。
概念1的一个例子是终对象定义中的性质。其中关于对于任意 for each,for every, for all 的对象
而关于图象的概念出现在我们考察某些范畴
对于“每个”、"对于每个 "或 "对于所有",使我们把它称为普遍属性:对象 1 是通过它与 "宇宙"(即我们所考虑的范畴)中的每个对象的关系来描述的。
以下是这段话的翻译:
“在研究某个范畴
如果范畴
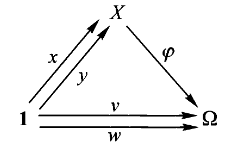
集合的范畴有一个特殊性质,大致是因为对象没有结构:如果两个映射在点上一致,那么它们就是同一个映射。也就是说,假设
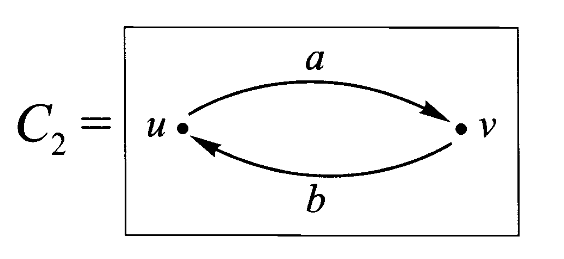
集合范畴的这个特殊性质在自态射范畴和图范畴中并不成立。例如,在自态射范畴中,2-环
当然还有其他形状的图。在集合范畴中,
但如果
集合范畴的这个特殊性质可以看成是只用很小的一族形状(只需要
2、自态射范畴中的类似性质
在自态射范畴中我们是否能找到可以用来探测其他对象的一小族图形呢?先前我们知道循环自态射
如果
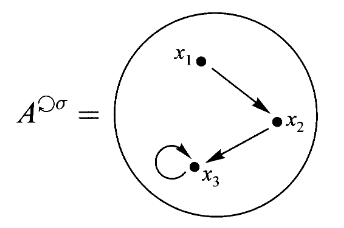
在
例如从
显然
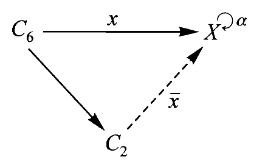
显然若
现在让我们考虑
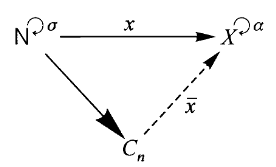
那么这说明在
这张图中的粗箭头表示满态射,也就是说至多有一个
在我们笔记中如果有需要,用
来表示单态射,用 来表示满态射。
回到
我们知道在集合范畴中只需要
3、相交关系 incidence relations
假设
这是否意味着
或者更大,比如
4、图范畴中的基本图形、奇异图形、相交关系
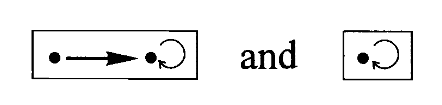
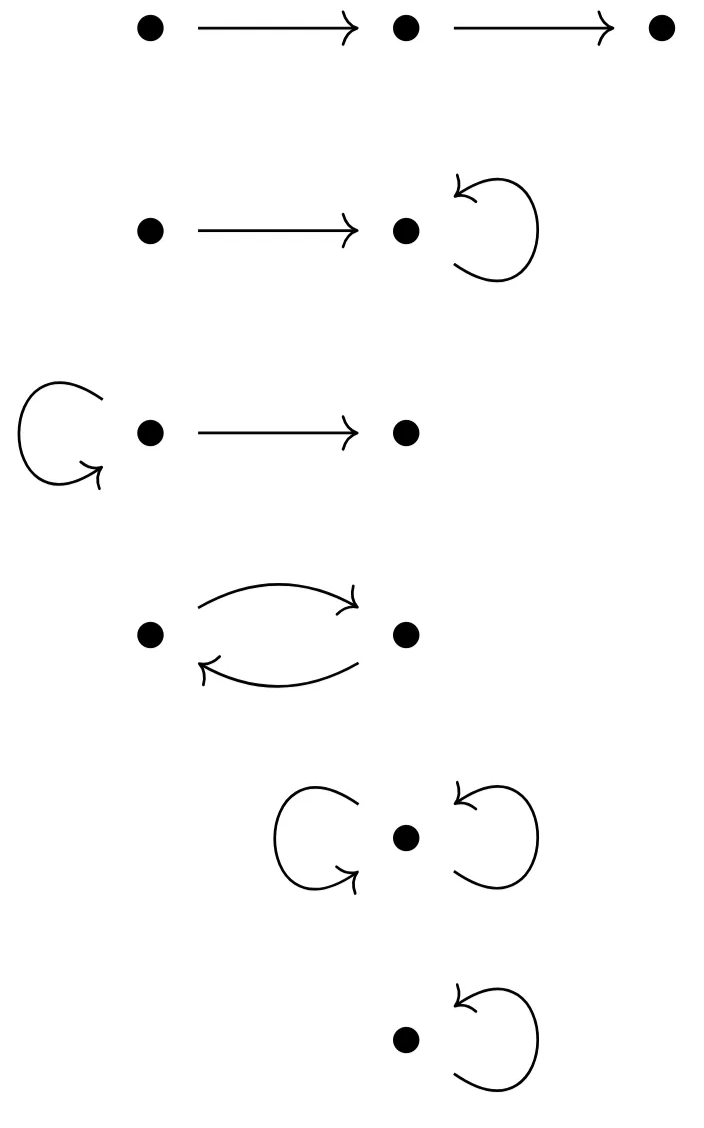
我们来考虑图范畴的情况。在该范畴中有两个对象可以作为基本形状,分别是孤立点
在图范畴中我们有以下性质(基本图形的规定性):给定任意一对映射
在集合范畴中我们需要
形图来区分映射,在自态射范畴中我们需要一个更大的 -形图来区分映射,而在图范畴中我们则需要两个图形来区分映射。
练习1:考虑图范畴中的映射
证明:泛性质的一部分,即对任意
现在让我们加上与
我们构造
- 对任意节点
, - 对任意箭头
,
这个定义意味着
由前面节点和箭头的任意性以及二者与
另一种有用的图形是下面这种
它有两个箭头,因此有两个
为了表达这种相交性,我们回忆从
那么这种相交性可以表示为下面的交换图
即
虽然不需要,但容易猜到就是满足上述交换图的
只有 。
如果某个对象
,即满足
注意这是
的一个泛性质。如果我们试图推广一下这个结论就是, 是满足该交换图性质的那个“最小”对象,使得对任意满足该交换图性质的对象 内部都能找到 -形图,也就是说这个对象满足了一种泛性质。换言之如果 中存在两箭头相交于一点,那么 中必然存在 -形图。这个最小性使人莫名联想到公因子性质。
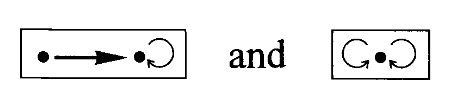
或者箭头塌缩
这里原书点塌缩左边的例子画错了,应该是单箭头
的图。
练习2:列举
解答:
类似的我们可以构造出许多满足各种泛性质的对象,比如上面的
即箭头
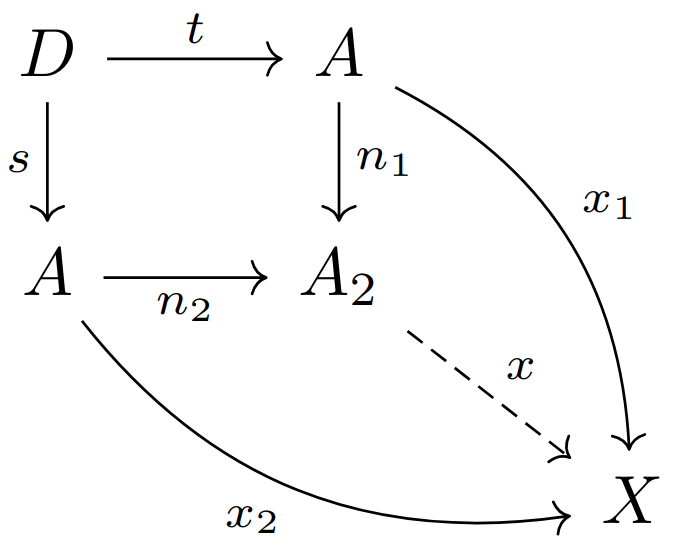
现在回到我们在第十五讲埋下的问题,即图范畴的表示。我们可以回答这个问题,因为我们所需要的理论工具正好就是图像 figure 和相交关系 incidence relations。
设
- 某箭头与某箭头同源
- 某箭头与某箭头同汇
- 某箭头与某箭头源汇相接
- 某箭头源为某点
- 某箭头汇为某点
这些节点列表与相交关系方程组合称为图
那么是否任何图的表示都至少要列出所有的箭头呢?是否能找到任意有限图的最小表示?
这里我们又揭示了表示与泛性质的联系。表示是一种交换图性质。我们可以猜想在任何范畴里,对象
的表示是这样一种交换图,若任意对象 满足该交换图,则存在唯一的 -形图 满足交换图的对应。
第二十三讲、更多泛性质
关于各种各样的泛性质,我们可以罗列出下表:
| 始对象 | 终对象 |
|---|---|
| 对象的和 | 对象的积 |
| … | 指数、幂、映射空间map space |
该表划分成两列,因为泛性质总是成对出现。左右两列相互对应,区别在于所涉及的泛性质中的箭头倒转,定义域与陪域互换。
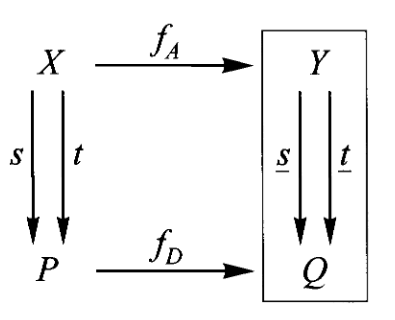
1、映射对范畴
给定范畴
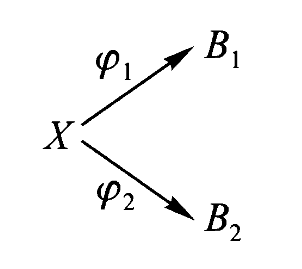
而范畴中的映射即图示间的映射,满足保持结构的性质,即使下图交换:
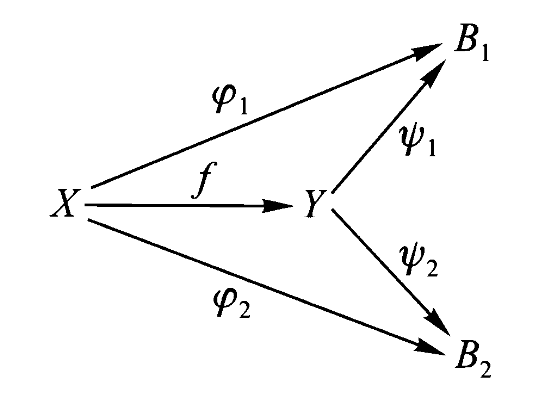
由此,我们可以把
练习1:借助这种等价性证明积对象的唯一性。
解答:略。
2、如何计算积
正如我们无法区分(不如说是范畴无法区分)任何两个终对象,因此我们称其中任何一个为那个(the,即从不定冠词a过渡到定冠词,表示终对象总是特指的那一个,即唯一性)终对象。同样的我们也称那个积对象。
根据积的泛性质可知,给定任意到因子
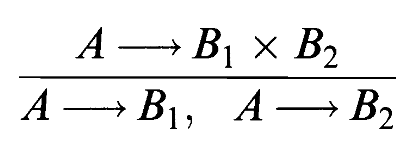
特别的,如果我们在集合范畴下,可以考虑
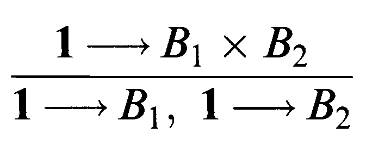
也就是说,只要我们知道了因子中的每个点,我们就知道了积对象中的每个点。
用类似的方法可以计算其他范畴中的积对象,只需要把
前者确定了
后者确定了
综上
注意到从内部结构上说,
练习2:尝试将积的泛性质中的箭头倒转定义其对偶概念,和。然后验证在集合与图范畴中,和就是无交并。
解答:略。见第四章第6节中的练习17。
第二十四讲、积的唯一性与和的定义
1、终对象是积的恒等元
注意原文构造
2、积的唯一性
略
3、对象的和
定义略。和的泛性质中诱导出的唯一映射
这个记号相当于一种分类讨论的意味,即
在图范畴中,
于是我们可以写出图范畴中的一些代数方程 algebraic equations。
练习2:证明图范畴中的下列公式
解答:
- 显然两边都只有两个节点,且左边没有箭头。但是对于右边来说是否有箭头呢?如果有,那么就有从
的箭头集合到 的箭头集合的映射,然而 的箭头集合是空集,因此不存在这种映射,故不存在箭头。 - 显然。
- 两边只有两个节点。至于没有箭头的理由同a。
练习3:重读第十五讲第5节,找到从
解答:
显然,只要知道二者的表示(生成元和生成关系),把它们罗列在一起即可。换言之,若记
为 的生成元, 为 的生成元,则 为 中的生成元,相应的生成关系则是把方程中相应的生成元替换成入射像,把相关的自态射替换成 ,其中 ,例如 替换成 。 我们先从最简单的情况开始分析,考虑
的表示。其中 的表示为生成元 ,生成关系 , 的表示为生成元 ,生成关系 。那么 的生成元就必然由 与 生成元的所决定,即 ,那么 应该满足什么生成关系呢?我们进一步考虑 的情形。记积对象上的自态射为 ,那么我们有 其中,每一列
表示 。因此我们发现 。 更一般的,当
不互素时,生成元 满足生成关系 。(见第二十一讲练习2)。 对于更一般的两个生成元
满足生成关系 ,此时如果要考察形如 的生成关系,则相当于 之类的方程成立,而这种情况是非常凑巧的。也就是说对更一般的生成元,我们先穷尽所有生成元的组合 (这里要么 是生成元,要么 是生成元),然后考虑序列 ,然后用所有生成关系 去约简,如果能够约简出 这种方程,则找到一种生成关系。总之没有本质上的困难,只是必须具体情况具体分析,而无法给出普遍形式。 试举一例:
此处,两个因子各只有一个生成元,分别为
,生成关系分别为 。而 由此例可以见得,积对象的生成元并不总是由因子对象中的生成元构成,例如此处不仅仅包括
,还有 。总之至少含一个生成元,这是因为对任意一个积对象中的点 ,它必然经过某个生成元若干步转移后得到,不妨设为 ,那么 ,也就是说 的生成元至少需要满足其中有一个分量在因子中是生成元。在罗列出全部此种形式的点以后,再用转移映射 不断作用其上最后根据生成关系约简即可得到积对象上的全部生成关系。
第二十五讲、标签与图的积
在积的泛性质中,
不是积,那么只需要找到一个
说明
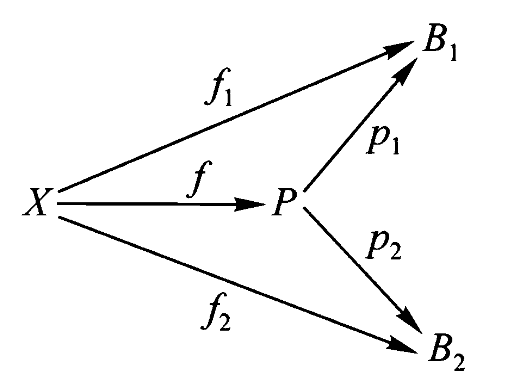
使该交换图成立的
1、通过标签探测图的结构
我们回忆所谓的标签labeling就是分拣sorting,就是把一个待考察对象
类似的,如果存在从
反之,如果我们能把
相似的问题是:用
这就是说,从
再举一例:用
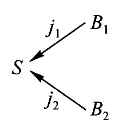
在这种情形下,对
练习1:找一个图并记为
解答:考虑下图
该图把
在做此题时我有过犹豫,似乎能把
中的箭头分成两类的 有许多不同选择(在同构意义下)。但如果有不同选择的话,就会对练习2b中的证明造成影响。因此我的想法是 的性质应该与 接近,也就是说对任意的 都到 有映射,即不存在结构上的限制,只是单纯的进行分拣。
如果我们把
下面的练习2b就是第二十二讲中的练习1的对偶。
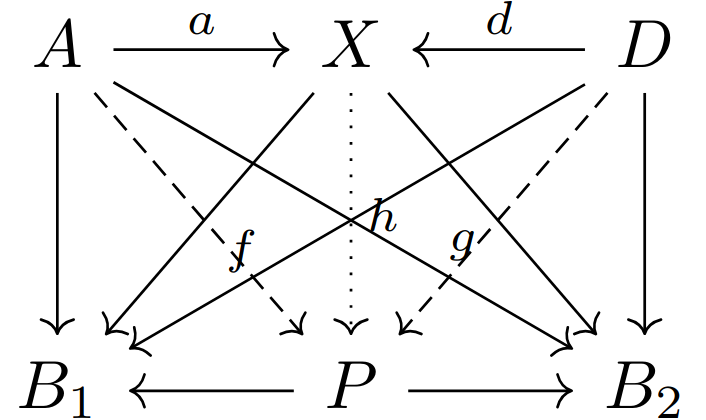
练习2:
- 证明在集合范畴中若上图对
满足余积的性质,则它实际上是就是真正的余积,即对任意对象 都满足余积性质。 - 证明在图范畴中若上图对
满足余积性质,则它实际上是就是真正的余积,即对任意对象 都满足余积性质。
解答:
在证明以前,我们不妨回顾一下其对偶命题的证明。即证明在集合范畴下,若积的泛性质仅对
成立,则它事实上对任意对象 成立。在那里对于任意 与映射 ,像点 规定了两个映射 ,因此诱导出唯一的 ,从而只要规定 为 ,即满足 的 即可, 的唯一性由 给出。 下面来证明2a。因为对于任意映射
,存在唯一的映射 使得和性质成立。我们证明首先证明 一定是单射,这是因为假如存在 ,那么可以构造映射 就违背了泛性质,类似的可以证明 也是单射且 的像不重合。进一步我们可以证明 ,由于集合范畴的同构性,这就是说 的元素数目必须与 和 的元素数目和相等。因为前面已经证明了 为单射且像不重合,因此 。然而若 ,则必然存在 既非 也非 的像,因此对于任意满足和泛性质中的交换图映射 ,总可以构造另一个不同的 ,使得 ,因此这与和的泛性质中导出映射的唯一性矛盾。综上可知 即 。 一旦证明
,就容易构造对任意 满足条件的唯一导出映射 。只需要令 即可,这种赋值的无矛盾性就在于无交并的特性。 证明2b的方式和2a非常相似。首先依旧是证明
是单射,只不过这次是图范畴中的单射,也就是说在节点集合上的映射 是单射(任意两个不同节点的像不同),在箭头集合上的映射 也是单射(任意两个不同箭头的像也不同)。证明前者只需要对 ,对任意 构造 满足 即可,根据 的性质这种构造总是可能的,因为 对图 的结构没有任何限制,也就是说对 之间有没有边,有几条边,边的结构如何没有任何限制,总是存在这样的保持结构的 。同理根据 的性质可以证明箭头集合也是单射,以及 的像不重合。同样的我们可以分别证明 ,也就是说 ,即它是两个图的无交并(两个图的无交并就是把两个图的节点集合无交并,再把箭头集合无交并得到)。同理对任意 容易构造满足条件的唯一导出映射 。
练习3:三色染(tricoloring)指的是为图中每个节点染上白、红、绿其中一色,使得对任意的箭头而言,其源节点和汇节点不同色。若我们固定一个图
- 证明被诱导的三色染确实满足三色染的定义,即对
中任意箭头而言,其源节点和汇节点不同色。 - 找到最佳三色染图
,即对任意的 ,任意 的一种三色染由唯一的映射 导出。
解答:
反证法,假设存在
中的某一箭头 , 颜色相同,那么根据诱导性质 同色。但由于 是图映射,它必然将 映射到 中的箭头 ,于是 在 中就是一个源汇节点同色的箭头,与 固定的三色染矛盾。 取
如下 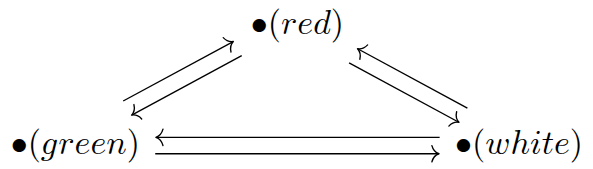
注意b不是对任意的
成立,而是对那些任意具有三色染的 成立。(不具有三色染的例子很多,只要它包含一个完全4-子图即可)。若 具有三色染,则显然可以通过把对应的颜色映射到 中的对应点即可,即若 为红色,则令 ,以此类推(映射 的存在性)。至于映射的唯一性,则因为若存在 都导出同一种三色染,则对任意的 , 与 同色,根据前面导出映射的性质, (因为同色像只有一个点,故相等),因此映射是唯一的。 这里之所以要在三个点之间两两构造箭头,是为了穷尽三色染中的所有边的可能性(由红到绿,由绿到红,由白到绿,由绿到白,由白到红,由红到白),从而任意三色染到
的映射只需要考虑节点的映射,而箭头映射总是自动良定义的(即保持结构)。
练习4:记
- 要么存在一个映射
,要么存在一个映射 ,且二者不同时成立; - 要么存在一个映射
,要么存在一个映射 ,且二者不同时成立; - 要么存在一个映射
,要么存在一个映射 ,且二者不同时成立;
这个序列是否能够继续下去?即是否存在某个图
d. 要么存在一个映射
解答:
- 满足前半句的是空图
,只要图 非空,就必然存在至少一个节点,于是满足后半句。 - 满足前半句的是无箭头图;只要图
有一个箭头,就满足后半句。 - 满足前半句的是只含头尾不相连的箭头图(即图中的点要么为孤立点,要么只是某个箭头的源节点,要么只是某个箭头的汇节点);只要图
有头尾相连的箭头(要么一个环,要么有一个节点既是源节点又是汇节点)就可以把 嵌入,于是满足后半句。 - 对于 d,我们首先说明只需要考虑连通图即可(如果图中有多个连通分支,那么就研究每个连通分支满足前半句还是后半句,若所有连通分支都满足前半句,则总体满足前半句,若有一个不满足前半句,则总体都不满足前半句)。于是问题变成,不满足前半句的连通图长什么样子,这些连通图是否可以通过找到一个合适的
统统被后半句刻画?我们观察发现满足前半句的连通图至多有一个节点既是源节点又是汇节点,那么除此以外的连通图就至少有两个节点既是源节点又是汇节点——于是可以取 (此处省略图示,不言而喻)。
此题告诉我们,任何图都可以被
划分成不相交的两类,要么它可以经过 的折叠并嵌入,要么它可以嵌入 。
2、计算图
如我们前面看到的,形如
即
这意味着
为确定
再举一个复杂的例子:
练习5:记
解答:
显然二者都等于
该练习告诉我们积的消去律一般不成立,哪怕其因子比之前见过的反例更为实质性substantial。其他的反例还有
。
3、分配律
练习6:构造映射
解答:略。我们在第四章分配律一节已经构造了。
注意该映射不一定是同构。
第二十六讲、分配范畴和线性范畴
1、标准映射
上一讲的练习要求我们求这个标准映射(之所以使用标准一词是因为该映射在运用和、积对象的泛性质推理过程中是唯一的)。在许多范畴中该映射与另一个标准映射
若一个范畴不是分配范畴,则我们避免在该范畴中使用“和”(sum)这个术语,而是代之以“余积”(coproduct),取“积的对偶”意义 。一个范畴不同于另一个范畴的根本区别之一是其概念concepts与余概念coconcepts之间的关系。在许多范畴中,分配律是有效的,但在其他范畴中,乘积和共乘积之间的关系却截然不同,但却同样有趣。
上述的标准映射的构造是一个普遍事实的应用——即把积的泛性质与余积的泛性质结合起来:
从两个对象的余积到两个对象的积的映射“等价”于四个映射,即从每个加数到每个乘数的映射。
由于余积对象是定义域,因此任何一个从
而
所以最终
反过来,这四个组分决定了从
而通常我们更倾向于将其写成矩阵 matrix 形式,即
同样的方法可以应用于任意数目的对象的积与余积上:
命题:对任意对象
其中
满足所有
证明:注意在这个命题中
- 先利用陪域是积再利用定义域是和的性质。即固定
而遍历 ,则所有 的存在性根据积对象的性质诱导出 的存在性,然后遍历 ,所有 的存在性根据和对象的性质诱导出 的存在性。其中 。 - 先利用定义域是和再利用陪域是积的性质。即固定
而遍历 ,则所有 的存在性根据和对象的性质诱导出 的存在性,然后遍历 ,所有 的存在性根据和对象的性质诱导出 的存在性。其中 。
无论哪一种我们都证明了
如果要用这个命题来定义上面的标准映射
为此我们需要先定义这四个映射。左边两个只需要使用积投射,而右边两个则使用积投射与和注射的复合,即
由此我们就得到了标准映射。在集合范畴下,它可以图示化为
这个标准映射的构造对所有范畴均成立。更一般的,我们可以构造标准映射
定义1:若对任意的
定义2:若范畴中的标准映射
定理:若范畴满足一般分配律,则范畴为分配范畴。反之若范畴为分配范畴,则其满足一般分配律。
即上面两个定义等价。
证明:
定义1推定义2:显然取
即可。 定义2推定义1:当
时,已知。当 时,显然。当 时,用数学归纳法:假设含 项的分配律成立,则对 项的分配律而言有 其中第一个同构使用了和的结合律(随便加括号,析出前
项与最后一项),第二个同构使用了二项分配律,第三个同构使用了 项分配律,第四个同构再次使用了和的结合律。于是 项分配律也成立,数学归纳法成立。证毕。
在第五章我们会讲到指数对象 exponential objects,我们将证明任意含有指数对象的范畴都是分配的。
有哪些范畴不满足分配律呢?例如第四章中的练习20中的带点集范畴。此外还有一类重要的范畴称为线性范畴 linear categories,其中积对象
2、线性范畴中的矩阵乘法
现在让我们稍稍偏离主题,讲讲关于线性范畴的一二事。首先在线性范畴中需要定义零映射。
定义(零映射):对任意两个对象
零映射的存在性使我们可以定义从
前面我们提到标准映射存在的重要条件是映射
对每个组分都存在,这里零映射的存在性就保证了这一点。
我们称该映射为恒等矩阵。(注意它与线性代数中矩阵的形式相似性)
定义:若一个含零映射的范畴中所有恒等矩阵都是同构映射,则该范畴称为一个线性范畴(linear category)。
在线性范畴中由于恒等矩阵可逆,我们因此可以对任意两个矩阵作乘法,即
其中,矩阵的乘积是
而
3、线性范畴中的映射加法
上述的矩阵乘积有一个有趣的结果。若
我们可以证明这两个矩阵的乘积必然形如
其中
首先由下图可知,标准映射
有两种表示
满足: 我们可以将其简记为,
取第一列(对应 的那一列), 取第二列(对应 的那一列), 取第一行(对应 的那一行), 取第二行(对应 的那一行)。 类似的由下图可知如上构造的恒等矩阵
有两种表示
其中逆映射
满足 展开乘积为复合:
分别计算其四个分量:
因此
练习1:借助上述矩阵乘积与映射加法的定义,证明下面矩阵乘法的公式:
为了便于证明,我们首先引入三个引理:
引理1:
这两个等式易证——只需要画出和与积泛性质的交换图即可。
引理2:
这在上面已经证明了。
引理3:标准映射
这在上面也已经证明了。
下面是正式的证明。类似前面的证明,我们只需要分别证明四个分量即可。例如对于左上角分量要证明:
其中
根据映射的和的定义,我们知道
因此待证之式为
等价的就要证明
我们颠倒了后者的分量顺序,等价性由自然同构
保证。
我们受通常的矩阵乘法启发,将上式的证明归结为以下连等式:
即以下路径之间的等价性:
其中
,函数乘法 等于函数的复合 ,等等。
下面我们依次证明等式:
等式一其实要证
相当于
要证左右相等,即证明两个组分相同,即两边同时右复合注射
后相等 其中根据引理知,
等式二其实要证
相当于
要证左右相等,即证明两个组分相同,即两边同时左复合投射
后相等 其中根据引理知
因此
等式三其实要证
相当于
其中我们把
按引理三写成第二形式。此时我们发现不需要额外证明两个组分相同,因为我们直接有 等式四其实要证
相当于
要证左右相等,即证明两个组分相同,即两边同时右复合注射
后相等 综上我们对原矩阵左上角的组分证明了等式,最后类似的证明其他三个组分即可。证毕。
注意在证明过程中我们在记号上没有区分注射和投射的定义域,例如在第四部分的证明中,前面的
是 的注射,后面的 则是 的注射。
值得一提的是零映射的来由。在线性范畴中,有限族中对象的积与余积同构(反复使用两个对象的标准映射的同构性即可),特别的,若对空族而言,这就意味着终对象与始对象同构,因此任意两个对象之间的零映射都可以唯一的构造为
书中似乎没有证明这一点。抑或是说我们“规定”空族的积为终对象,余积为始对象(正如我们规定空族的数的乘积为1而和为0)。同时书中的线性范畴定义也没有显式说明其同构性对空族成立,它只是说两个对象的余积到积的标准映射同构,并没有把空族的底层情况(bottom case)考虑在内。
练习2:证明一个具有始对象与终对象的范畴中有零映射当且仅当始对象与终对象同构。
证明:充分性:如上面构造,显然。必要性:所谓范畴有零映射是指其中任意对象之间都有零映射,因此始对象与终对象之间也有零映射,因此
注意该证明中其实只使用了零映射作为一个特殊映射的普遍存在性,而
的存在性则是由始对象与终对象的泛性质保证的,因此真正使用到零映射存在性的就是 的存在性。
最后书上写到为了比较分配范畴和线性范畴,我们把矩阵写成了与以往不同的形式(转置形式)。
但是这句话没头没尾的,没看懂。
4、和与积的结合律
这里我们已经证明过了。略。
我们从任意族对象的积与和的定义出发证明空族的积为终对象,和为始对象。回顾第四章第五节中积的定义:对一个指标族
由此我们知道,当指标集
第二十七讲、泛构造举例
1、泛构造 universal construction
我们已经看到两种泛构造:与积对象、终对象相似的构造,术语叫做极限 limit,还有与和对象、始对象相似的构造,术语叫做余极限 colimit。我们可以总结如下:
| 余极限 | 极限 |
|---|---|
| 始对象 | 终对象 |
| 两个对象的和 | 两个对象的积 |
| 三个对象的和等等 | 三个对象的积等等 |
后文略。
2、对象有相反对象吗? Can objects have negatives?
对数而言,3的相反数定义为方程
方程中的每个符号
这个结论是否能推广到任意范畴中呢?
命题1:对任意含有始对象的范畴中的两个对象
证明:因为
- 存在性:因为
是始对象,因此对任意 存在 ,那么又因为有注射 ,因此 是这样一个映射。 - 唯一性:假设
是另一个映射,由于和的泛性质,映射对 存在唯一的映射 使得 ,而因为 是始对象,因此 ,于是 。
由此可知
因此我们可以说只有始对象有相反对象。
命题2:对任意含有终对象的范畴中的两个对象
证明:因为
- 存在性:因为
是终对象,因此对任意 存在 ,那么又因为有投射 ,因此 是这样一个映射。 - 唯一性:假设
是另一个映射,由于积的泛性质,映射对 存在唯一的映射 使得 ,而因为 是始对象,因此 ,于是 。
由此可知
类似的可以说只有终对象有倒 reciprocal 对象。
3、幂等对象
考虑使得
这里说至多只有一个,是因为积的泛性质中是对任意到
上有映射的对象 而言,也即它并未假定对任意对象 都有到 的映射的存在性。但是如果存在则唯一,这就是至多只有一个。
练习2:
- 上述结论的逆命题。若
满足对任意对象 至多只有一个映射 ,则 是一个积。 - 证明上述性质等价于:映射
是单态射。
证明:(a) 显然。导出映射只能是
练习3:找出集合范畴、自态射范畴、图范畴中的满足上述性质的对象
解答:根据2b的结论,只要找出所有到终对象的映射为单态射的对象即可。在集合范畴中,终对象是单元集,因此只有空集和终对象本身。在自态射范畴中,终对象是单点自态射集,因此只有空集和终对象本身。在图范畴中,终对象是但单节点自环,因此有空集,孤立点集和终对象本身。
是否存在满足
有的。最有趣的例子莫过于Cantor在对角线证明中构造的同构
与同构
即
练习4:上述同构映射
- 请计算出对应的系数。
- 请证明由该式与相应系数定义的公式是一个同构。
- 无论同构
取什么形式(即不按照上面的对角线法则的话), 都不可能用一个多项式给出解析形式。
证明:
我们先证明
的必要形式,即如果 是这样一个同构,它只能是什么形式。因为它只有5个待定系数,取 的前几项构造线性方程组: 解得
,即 。 我们只需证明
既单且满。 单射性:若
,则我们可以推出 其中
。由于 均为自然数,因此若要两边在 都不为0的情况下相等, 必须整除 ,因此 。若 ,则 ,若 则右边系数为 ,因此 ,因为 ,因此 中恰好只有一个为 其余为 ,但无论哪种组合要么 ,要么 ,无论那种情况都与 矛盾。综上, 只能是 即 ,即单射性成立。 满射性:为方便叙述,我们将集合
称为第 条对角线。注意到第 条对角线上的元素按照 的顺序遍历 区间上的 个自然数。因此满射性成立。 假设
满足 且 为关于 的多项式。根据 可知, ,解出 显然它蕴含了根号项(该项为0等价于
,但代入发现显然不能使得 为同构。
4、解方程、画映射
在几何学、代数学、逻辑学等明确使用范畴论的书籍中,都讨论过极限和余极限的一般概念。特殊情形下,积是从给定的对象族中提取出单个对象,而更一般的构造则从给定的涉及对象和映射的图示 diagram 中提取单个对象。一个重要的例子是形如
定义:称
练习5(等化子的唯一性):若
证明:由
练习6:任何映射
证明:要证明
练习7:若
证明:要证明
练习8:任意集合范畴中的平行映射对
解答:换用图范畴惯用的记号
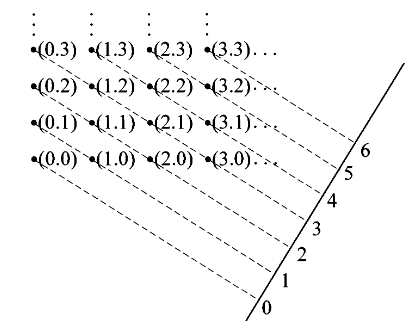
图 graph 一词在数学和其他领域的另一个非常重要的用法是描述特定函数具体行为的某种图像 picture。如果我们可以描绘笛卡尔积,我们可以就从下面的图形中得出这种图像。
考虑投射
练习9:对任意映射
证明:显然取
该截面映射
练习10:在含有积结构的范畴中(例如集合范畴),给定两个平行映射
解答:这里没有要求我们严格证明,只是解释。所以不妨就限制在集合范畴内。首先图像的交集为
我们在本书中经常使用的特定映射
请尝试着把等化子的定义对偶化,以得到“余等化子” coequalizer 的概念,并解释为什么把集合范畴中的平行映射看作源-汇结构时,余等化子就成了图的“分支集合” set of components。
练习11:称
证明:该命题是练习6的对偶形式。若要证明
练习12:对给定映射
解答:
这个练习12描述的不清不楚。通过询问GPT,我们得知这个泛结构被称为核对,即要找到
中所有被 映射到同一个像点的元素对 。(这里请不要按照集合的元素来理解,因为正如我们早先提到的,在范畴中我们用映射讨论一切,而此处 是从 到 的映射。
首先我们来定义
下面证明
- 自反性:即把平行映射对
视为图时,满足第三部分第三章第8节自反图的定义,即存在态射 ,使得 。这是因为 满足 的性质,因此根据 的泛性质,存在 使得 。 - 对称性:即存在对合映射
使得 。这也显然,因为 与 满足的是相同的性质,因此由泛性质知存在这样的 。复合两次 我们就得到 ,而第一个和最后一个 的平行映射对顺序一致,因此二者间存在唯一的映射(即恒等映射),于是知道 ,即其为对合映射。 - 传递性:给定三个态射
,若 则 。即若 满足上述条件,则 也满足上述条件。这是显然的。 - 联合单射性:我们记
。对任意 ,它都诱导了两个映射 ,这两者分别对应了两张图 。若 ,记 ,则这两张图都满足存在唯一的 使得 ,而 都满足唯一的 的性质,因此 。证毕。
第二十八讲、带点集范畴
1、非分配范畴的例子
带点集范畴。其范畴映射的特点是映射把基点映射到基点。因此带点集的积对象中的基点的投射必须是两个乘数中的基点,而带点集和对象中的基点则是两个加数中基点的注射,因此带点集的和相当于是把两个带点集的基点粘接在一起。
练习1:分配律的两个部分在带点集范畴中均不成立。
- 找到对象
使得 不为同构。 - 找到对象
使得标准映射 不为同构。
解答:
- 考虑
,因为 ,因此 显然二者不同构。 - 考虑
,则 而 ,显然二者不同构。
练习2:我们看到在带点集范畴中,映射
解答:根据任意两个对象之间的零映射
测试三
练习1、2显然,略。
练习3:在图范畴中,请刻画
解答:
测试四
练习1在第二十七讲第2节作为和为0的对偶命题已经证明过。
练习2:在图范畴中
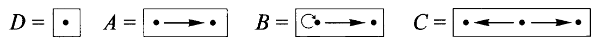
- 找到
的映射个数与 的映射个数。 - 计算(画出内部表示)
。 - 根据分配律与(b)的结果,计算
。 - 证明
。
解答:
前者只有一个,后者没有。
简便起见把三张图画在了一起。最底下是
,最左侧由下至上分别是 ,右侧两列由下至上分别是 。 
如图。
如图显然。
由 a,d 可知消去律不成立。
测试五
练习1:找到尽可能多的两两不同构的图,恰好包含四个节点和两个箭头。提示:这种图的数量介于10到15个之间。
解答:
我只想到这11个,应该覆盖了全部情况。
练习2:记
解答:由下图知,
第二十九讲、二元运算与对角线方法 Binary operations and diagonal arguments
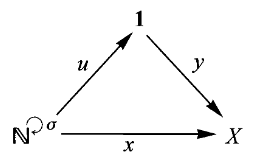
从某种意义上说满足泛性质的对象,如果从一边看是平凡的,但如果从另一边看就不是平凡的了。例如,从一个对象到终对象
1、二元运算和作用
本节课我们将研究将积映射到对象的两种重要情况。第一种情况是三个对象相同,即映射
二元运算的例子可以在算术运算中找到。例如,若
类似的可以定义乘法。如果我们不能定义笛卡尔积
当然,关于二元运算还有很多内容要讲。正如我们在第四讲中看到的,二元运算本身就是一个范畴,而且是许多研究的主题。
另一个重要的情况是作用,即
另一方面,我们可以按下一个不同的按钮。因此一个作用并不只涉及一个自态射,而是一系列不同的自态射
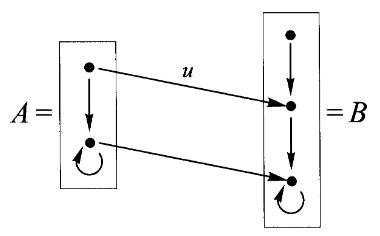
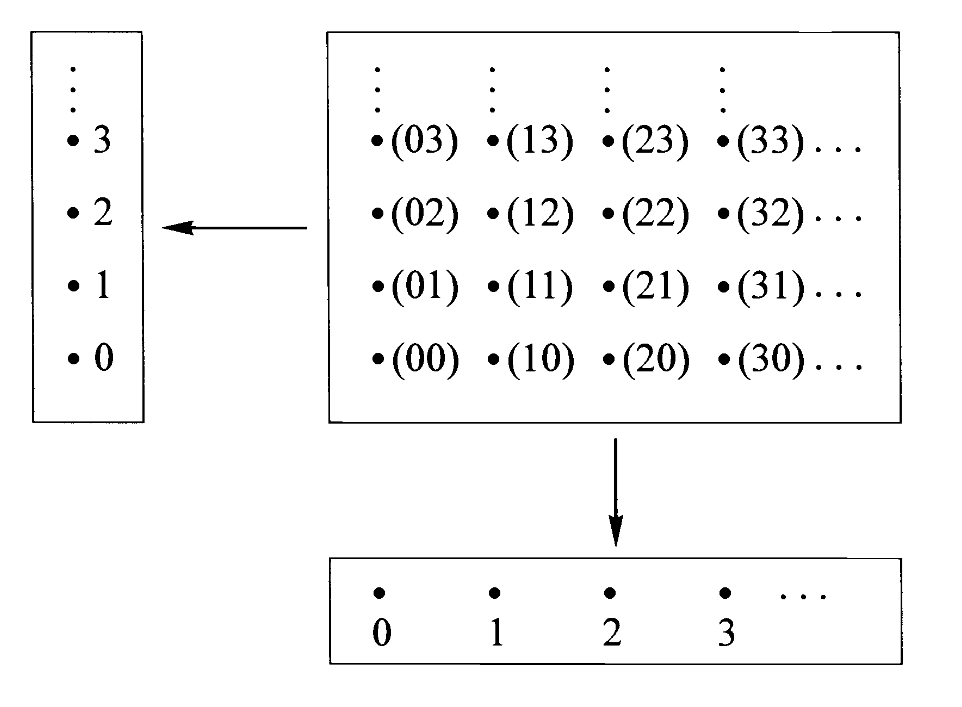
2、康托尔 Cantor 的对角线方法
从一个积对象出发的映射最一般的情形是所涉及的三个对象都不同:
每个点
因此
对角线定理:在任何含有积结构的范畴中,若
证明:假设
该映射对任意
我们已经假定每个映射
这个证明之所以被称为对角线方法因为其中对角线映射的作用,同时自态射
逆否命题:设对象
证明:用
在集合范畴中,有许多这种没有不动点自态射的对象
康托尔得到的结论是,对任意无穷集
练习1:如果仔细阅读康托尔的证明,就会发现它其实告诉了我们更多的东西。重写证明以说明如果
与
这个弱得多的例子可否举一例?
解答:因为题干中弱参数化的
之所以康托尔证明对弱版本也成立,是因为原命题中其实也是通过构造一个特殊点的取值来形成证明,因此只需要能够进行这种特殊点构造的条件就行了,即逐点一致的条件。
康托尔的对角线证明与著名的哥德尔不完备性定理紧密相连,哥德尔定理的设定是主观范畴 subjective categories。
我们对康托尔对角线定理的证明显然对任意含有积结构的范畴有效。罗素 Russell 在1900年左右以及哥德尔 Gödel 和塔斯基 Tarski 在20世纪30年代利用这一事实推导出了某些结果(有时在通俗书籍中被描述为“悖论”)。尤其是哥德尔的工作比康托尔的工作更进了几步。有一种常见的思路,并不是先把可能的动力系统或可能的图形等形象化,然后再试图理解这些对象及其变换。相反,这种思路是:
- 从公式和证明规则出发,并试图
- 只考虑那些可以用公式完全描述的映射(或图等等),以及
- 认为只有当相应的公式可以根据某些给定的规则证明等价时,两个映射才是相等的。
这部分“构造性”观点在数学上取得了一些进展,因为从客观上讲,它产生了一些新的范畴,这些范畴在某些方面与集合范畴、图范畴等非常相似,但在某些方面又截然不同。
我们将在第五部分更详细地看到在大多数范畴中,相关的真值不仅仅是两个
其中
如果证明规则不足以证明
康托尔对角线定理如何与罗素、哥德尔、塔斯基的这些思考相关联?若
这些映射在某种意义上能描述了所有可描述的属性
后面这个例子中的关键理想化(idealization)在于:我们假设所有属性(在给定句法方案中可描述的)都能以固定方式罗列出来,从而可以谈论“第3号属性”等。该列表可能形如:
(0)
(1)
(2)
(3)
(4)
(5)
等等。其中我们可以说
将成为
现在,由于所有映射
对每个
因为如果
建构主义者(也称为形式主义者,直觉主义者)的理想化“想象列出所有公式和所有证明”是非常合理的,前提是人们已经接受了“想象一个对象
关于理想化的科学过程,我们还应铭记另一位老友伽利略的伟大成就。这一过程包含两个同等重要的方面:其一,理想化本身往往意味着在众多作用力中,将某个“主导”力视为唯一作用力。伽利略研究落体运动时,这个主导力就是重力。此类理想化能推动理论取得深远发展——以重力理论为例,从伽利略、牛顿、雅可比、哈密顿到爱因斯坦,该理论始终运用于着地球与天体运行。前文讨论的案例中,被理想化的主导力则是(布劳威尔提出的)持续计数的冲动 urge。但理想化科学过程的第二个关键方面在于:将发展成熟的理论应用于新情境时,必须始终保持清醒认知——那些被理想化排除的“次要”作用力可能正在产生影响,甚至可能转化为新的“主导”力。伽利略深谙此理:若从比萨斜塔抛下的不是炮弹或木球,而是一片枯叶,摩擦力和风力将成为决定其坠落轨迹的关键因素;人们甚至可能观察到枯叶“逆升”的“悖论”现象。这并非说明纯粹重力理论有误,而是表明需要更全面的纯粹理论来解释该现象。鉴于计算机与软件发展过程中,“持续计数的冲动”之外的作用力显然举足轻重,罗素、布劳威尔、塔斯基、哥德尔、图灵(及近代逻辑学家与计算机科学家)构建的精妙理论,其纯粹形态的应用场景实则有限。计数是主观过程,而重力是客观作用力。即便应用目标涉及主观成分(如计算工程问题答案),客观作用力的影响同样不容忽视。
关于Lawvere对主客观范畴的哲学讨论在前文第六讲第三节就没太看懂,他似乎想引用马克思主义的主客观关系(或者矛盾论)来解释数学,或者反过来用数学来解释之。
不妨谈谈我的观点。我从哥德尔完备性定理(命题逻辑的完备性)与不完备性定理(蕴含一阶逻辑和自然数公理的系统不完备)上得到的最大启发是,自然数公理的那个继续计数的动力,就是辩证运动的一种极端的数学简化,即后继数总是不断的否定它的前驱达到一个新的、史无前例的状态,而这种动力就会突破一切既定的现有的形式逻辑框架,挣脱它的解释和约束,得到无法证明的真理。